Question

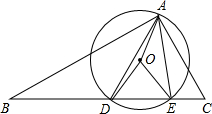已知△ABC中，∠BAC=90°，点D，E在BC边上，且BA=BE，CA=CD，作△ADE的外接圆⊙O并连接OA、OD、OE．
（1）求证：BO平分∠ABC；
（2）求证：∠DAO=90°-∠AED；
（3）求∠DOE的度数．

Answer 1

分析：（1）根据全等三角形的性质即可证明；
（2）根据等腰三角形的性质、圆周角定理即可证明；
（3）根据三角形的内角和定理以及等腰三角形的性质和圆周角定理进行计算．

解答：（1）证明：∵OA=OE，BO=BO，BA=BE，
∴△OAB≌△OEB，
∴∠ABO=∠EBO．
即BO平分∠ABC．

（2）证明：∵∠DAO=

180°-∠AOD

2

，
∠AOD=2∠AED，
∴∠DAO=90°-∠AED．

（3）解：∵BA=BE，CA=CD，
∴∠BAE=∠BEA，∠CAD=∠CDA．
∴∠BEA=

180°-∠ABC

2

，∠CDA=

180°-∠ACB

2

．
∴∠BEA+∠CDA=180°-

1

2

（∠ABC+∠ACB）=135°．
∴∠DAE=45°，
∴∠DOE=90°．

点评：综合运用了全等三角形的判定以及性质、三角形的内角和定理等．