题目内容
如图,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos∠BCD的值是( )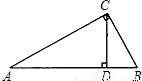
A.

B.

C.

D.

【答案】分析:易证∠BCD=∠A,则求cos∠BCD的值就可以转化为求∠A的三角函数值.从而转化为求△ABC的边长的比.
解答:解:由勾股定理得,AB= =
= =5.
=5.
由同角的余角相等知,∠BCD=∠A.
∴cos∠BCD=cos∠A= =
= .
.
故选D.
点评:本题考查了:①勾股定理;②锐角三角函数的定义;③同角的余角相等.并且注意到三角函数值只与角的大小有关.
解答:解:由勾股定理得,AB=
 =
= =5.
=5.由同角的余角相等知,∠BCD=∠A.
∴cos∠BCD=cos∠A=
 =
= .
.故选D.
点评:本题考查了:①勾股定理;②锐角三角函数的定义;③同角的余角相等.并且注意到三角函数值只与角的大小有关.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
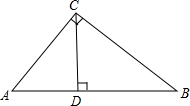 如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )
如图,CD是Rt△ABC斜边上的高.若AB=5,AC=3,则tan∠BCD为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
5、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( ) 18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于
18、如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于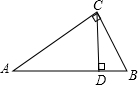 如图,CD是Rt△ABC斜边上的高线,若sinA=
如图,CD是Rt△ABC斜边上的高线,若sinA=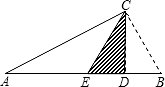 如图,CD是Rt△ABC斜边AB上的高,直角边AC=
如图,CD是Rt△ABC斜边AB上的高,直角边AC=