题目内容
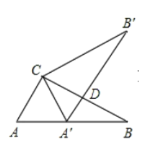
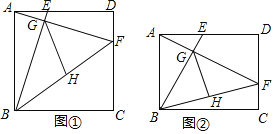
【题目】问题探究:如图①,在正方形![]() 中,点
中,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() .线段
.线段![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的中线.
的中线.
(1)求证:![]() ;
;
(2)线段![]() 与
与![]() 之间的数量关系为 .
之间的数量关系为 .
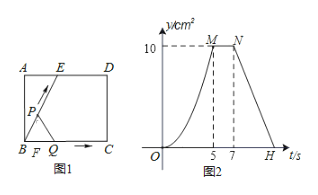
问题拓展:如图②,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,线段
,线段![]() 与
与![]() 相交于点
相交于点![]() .若
.若![]() 是
是![]() 的中线,则线段
的中线,则线段![]() 的长为 .
的长为 .
【答案】(1)详见解析;(2)![]() ,证明详见解析;问题拓展:
,证明详见解析;问题拓展:![]()
【解析】
(1)由正方形的性质得出∠BAD=∠D=90°,AB=DA,由SAS证明△ABE≌△DAF即可;
(2)由全等三角形的性质得出∠ABE=∠DAF,证出∠BGF=∠ABE+∠BAG=90°,在Rt△BFG中,由直角三角形斜边上的中线性质得出BF=2GH;
问题拓展:由三角函数得出∠ABE=∠DAF,证出∠BGF=90°,在Rt△BFG中,由直角三角形斜边上的中线性质得出BF=2GH,由矩形的性质得出∠C=90°,BC=AD=6,CD=AB=4,得出CF=CD-DF=1,由勾股定理求出BF=![]() ,即可得出GH的长.
,即可得出GH的长.
(1)证明:∵四边形ABCD是正方形,
∴∠BAD=∠D=90°,AB=DA,
在△ABE和△DAF中,
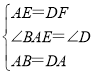 ,
,
∴△ABE≌△DAF(SAS);
(2)解:BF=2GH;理由如下:
∵△ABE≌△DAF,
∴∠ABE=∠DAF,
∵∠DAF+∠BAG=∠BAD=90°,
∴∠ABE+∠BAG=90°,
∴∠BGF=∠ABE+∠BAG=90°,
在Rt△BFG中,GH是边BF的中线,
∴BF=2GH;
问题拓展:
解:∵tan∠ABE=![]() ,tan∠DAF=
,tan∠DAF=![]() ,
,
∴∠ABE=∠DAF,
∵∠DAF+∠BAG=∠BAD=90°,
∴∠ABE+∠BAG=90°,
∴∠AGB=90°,
∴∠BGF=90°,
在Rt△BFG中,GH是边BF的中线,
∴BF=2GH,
∵四边形ABCD是矩形,
∴∠C=90°,BC=AD=6,CD=AB=4,
∴CF=CD-DF=1,
∴BF=![]() ,
,
∴GH=![]() BF=
BF=![]() ;
;
故答案为:![]() .
.