题目内容
如图，点D在AB上，点E在AC上，CD与BE相交于点O，且AD=AE，AB=AC．若∠B=20°，则∠C=考点：全等三角形的判定与性质
专题：几何图形问题
分析：在△BAE和△CAD中由∠A=∠A，AD=AE，AB=AC证明△BAE≌△CAD，于是得到∠B=∠C，结合题干条件即可求出∠C度数．
解答：解：在△BAE和△CAD中，
，
∴△BAE≌△CAD（SAS），
∴∠B=∠C，
∵∠B=20°，
∴∠C=20°，
故答案为20．
|
∴△BAE≌△CAD（SAS），
∴∠B=∠C，
∵∠B=20°，
∴∠C=20°，
故答案为20．
点评：本题主要考查全等三角形的判定与性质的知识点，解答本题的关键是熟练掌握两三角形全等的判定定理，此题难度一般．
练习册系列答案
相关题目
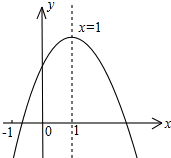已知二次函数y=ax2+bx+c（a≠0）的图象如图，下列结论：①abc＞0；②b＜a+c；③2a-b=0；④4a+2b+c＞0；⑤2c＜3b；⑥a+b＞m（am+b）（m为任意实数），
其中正确的结论有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
近年来，盐城房价不断上涨，市区某楼盘2013年10月份的房价平均每平方米为6400元，比2011年同期的房价平均每平方米上涨了2000元．假设这两年房价的平均增长率均为x，则关于的方程为（ ）
| A、（1+x）2=2000 |
| B、2000（1+x）2=6400 |
| C、（6400-2000）（1+x）=6400 |
| D、（6400-2000）（1+x）2=6400 |