题目内容
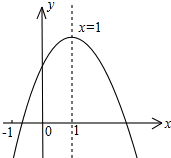 已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图,下列结论:①abc>0;②b<a+c;③2a-b=0;④4a+2b+c>0;⑤2c<3b;⑥a+b>m(am+b)(m为任意实数),
其中正确的结论有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:
分析:用二次函数图象的开口方向,对称轴,与x、y轴的交点,以及特殊的x=1、-1、2或-2的特殊值,进行判定(或推出)即可.
解答:解:①如图,抛物线开口方向向下,则a<0.
对称轴为x=-
=1,则b=-2a>0,
抛物线与y轴交点(0,c)的纵坐标c>0,
所以,abc<0.
故①错误;
②当x=-1时,y=a-b+c<0,所以b>a+c.
故②错误;
③由①知,b=-2a,则2a+b=0,
故④错误;
④当x=2时,y=4a+2b+c>0.
故④正确;
⑤因为a=-
b,又a-b+c<0,所以2c<3b.
故⑤正确;
⑥因为当m=1时,有最大值;
当m≠1时,有am2+bm+c<a+b+c,
所以a+b>m(am+b).
故⑥错误.
综上所知有2个正确的结论.
故选:B.
对称轴为x=-
| b |
| 2a |
抛物线与y轴交点(0,c)的纵坐标c>0,
所以,abc<0.
故①错误;
②当x=-1时,y=a-b+c<0,所以b>a+c.
故②错误;
③由①知,b=-2a,则2a+b=0,
故④错误;
④当x=2时,y=4a+2b+c>0.
故④正确;
⑤因为a=-
| 1 |
| 2 |
故⑤正确;
⑥因为当m=1时,有最大值;
当m≠1时,有am2+bm+c<a+b+c,
所以a+b>m(am+b).
故⑥错误.
综上所知有2个正确的结论.
故选:B.
点评:主要考查二次函数图象与二次函数系数之间的关系,注意抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点以及一些特殊的函数值.

练习册系列答案
相关题目
已知代数式3xaya+b与-5x3y2是同类项,则a-b的值是( )
| A、1 | B、2 | C、3 | D、4 |
计算(2a-3b)(2b+3a)的结果是( )
| A、4a2-9b2 |
| B、6a2-5ab-6b2 |
| C、6a2-5ab+6b2 |
| D、6a2-15ab+6b2 |
下列事件是不可能事件的是( )
| A、明天会下雨 |
| B、投掷一个骰子,5点向上 |
| C、任意选择电视的某一频道,正在播放新闻 |
| D、今年二十岁,明年十八岁 |
 如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,则∠C=
如图,点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.若∠B=20°,则∠C=