Question

【题目】如图所示，点I是的内心，AI的延长线交的外接圆于点D，交BC边于点E，

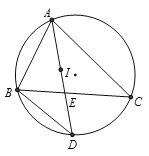
求证：（1）ID=BD

（2）BD2 =DA·ED

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）连接BI，由内心的性质得到∠1=∠2，∠3=∠4，而∠1=∠5，由此可得∠5=∠2，即可证明∠BID=∠IBD，由等角对等边即可得出结论；

（2）由（1）得∠5=∠2，易证得△BED∽△ABD，由此可得出所求的结论．

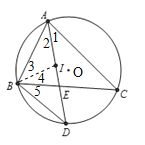
（1）连接BI．

∵I是△ABC的内心，∴∠1=∠2，∠3=∠4．

∵∠5=∠1，∴∠5=∠2．

∵∠BID=∠3+∠2，∠DBI=∠4+∠5，∴∠BID=∠DBI，∴ID=BD；

（2）由（1）得：∠5=∠2．

又∵∠D=∠D，∴△BDE∽△ADB，∴BD：DE=AD：BD；∴BD2=ADDE．