题目内容
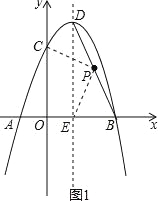
【题目】(2016广东省茂名市第25题)如图，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴DE交x轴于点E，连接BD．
（1）求经过A，B，C三点的抛物线的函数表达式；
（2）点P是线段BD上一点，当PE=PC时，求点P的坐标；
（3）在（2）的条件下，过点P作PF⊥x轴于点F，G为抛物线上一动点，M为x轴上一动点，N为直线PF上一动点，当以F、M、G为顶点的四边形是正方形时，请求出点M的坐标．
【答案】(1)、y=﹣x2+2x+3；(2)、（2，2）；(3)、（
，0），（
，0），（
，0），（
，0）．
【解析】
试题分析：(1)、利用待定系数法求出过A，B，C三点的抛物线的函数表达式；(2)、连接PC、PE，利用公式求出顶点D的坐标，利用待定系数法求出直线BD的解析式，设出点P的坐标为（x，﹣2x+6），利用勾股定理表示出PC2和PE2，根据题意列出方程，解方程求出x的值，计算求出点P的坐标；(3)、设点M的坐标为（a，0），表示出点G的坐标，根据正方形的性质列出方程，解方程即可．
试题解析：(1)、∵抛物线y=﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，
∴
， 解得，
， ∴经过A，B，C三点的抛物线的函数表达式为y=﹣x2+2x+3；
(2)、如图1，连接PC、PE， x=﹣
=﹣
=1， 当x=1时，y=4，
∴点D的坐标为（1，4）， 设直线BD的解析式为：y=mx+n，则
， 解得，
，
∴直线BD的解析式为y=﹣2x+6， 设点P的坐标为（x，﹣2x+6），
则PC2=x2+（3+2x﹣6）2，PE2=（x﹣1）2+（﹣2x+6）2， ∵PC=PE，
∴x2+（3+2x﹣6）2=（x﹣1）2+（﹣2x+6）2， 解得，x=2， 则y=﹣2×2+6=2， ∴点P的坐标为（2，2）；
(3)、设点M的坐标为（a，0），则点G的坐标为（a，﹣a2+2a+3），
∵以F、M、G为顶点的四边形是正方形， ∴FM=MG，即|2﹣a|=|﹣a2+2a+3|，
当2﹣a=﹣a2+2a+3时， 整理得，a2﹣3a﹣1=0， 解得，a=
，
当2﹣a=﹣（﹣a2+2a+3）时， 整理得，a2﹣a﹣5=0， 解得，a=
，
∴当以F、M、G为顶点的四边形是正方形时，点M的坐标为（，0），（，0），（，0），（，0）．
