题目内容
【题目】如图，正方形ABCD中，对角线AC上有一点P，连接BP、DP，过点P作PE⊥PB交CD于点E，连接BE．
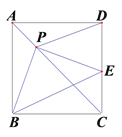
（1）求证：BP=EP；
（2）若CE=3，BE=6，求∠CPE的度数；
（3）探究AP、PC、BE之间的数量关系，并给予证明．
【答案】（1）证明见解析；（2）∠EBC=30°；（3）BE2＝AP2+PC2，理由见解析.
【解析】试题分析：（1）利用正方形的性质得出△CBP≌△CDP，得出BP＝DP，利用四边形的内角和，得出EP＝DP，从而得出结论；（2）取BE的中点F，得出△CEF是等边三角形，利用撒尿行内角和定理，得出∠EPC＝30°；（3）过点P作PC/⊥AC，得出△BPC≌△EPC/, 近而得出四边形ABEC/为平行四边形，在Rt△APC/中，利用勾股定理得出结论即可.
试题解析：
（1）∵ 四边形ABCD是正方形，∴CB＝CD，AC平分∠BCD， 即 ∠BCP＝∠DCP，
又CP是公共边 所以△CBP≌△CDP ∴ BP＝DP, ∠PBC＝∠PDC
∵ ∠BPE－∠BCE＝90°，∠BPE+∠BCE+∠PBC+∠PEC＝360°∴∠PBC+∠PEC＝90°
∵ ∠PED+∠PEC＝90°∴∠PED＝∠PBC∴∠PED＝∠PDC∴EP＝DP,
∴ BP＝DP ．
（2）取BE的中点F，连CF，则CE＝CF－EF＝3, ∴△CEF是等边三角形，则∠BEC＝60°，
∵∠BCE＝90°，∴∠EBC+∠BEC＝90°, ∴∠EBC ＝30°, ∵∠EBC+∠BCP＝∠PEB+∠EPC,
∠PEB＝∠BCP＝45°∴∠EBC ＝∠EPC＝30°﹒
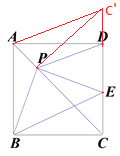
（3）过点P作PC/⊥AC，交CD的延长线于C/,得△BPC≌△EPC/, CP＝C/P,BC＝EC/,
∵AB＝BC，∴AB＝EC/∵AB∥EC/∴四边形ABEC/为平行四边形，∴AC/＝BE,
∵在Rt△APC/中，C/A2＝AP2+C/P2∴BE2＝AP2+PC2﹒
