题目内容
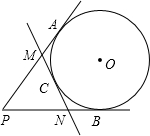PA、PB切⊙O于A、B，C为 |
| AB |
| A、5cm | B、6cm |
| C、8cm | D、10cm |
分析：由PA、PB切⊙O于A、B，MN切⊙O于C，根据切线长定理，即可求得AM=CM，CN=BN，PA=PB，又由△PMN的周长为10cm，即可求得切线长PA的长．
解答：解：∵PA、PB切⊙O于A、B，MN切⊙O于C，
∴AM=CM，CN=BN，PA=PB，
∵△PMN的周长为10cm，
即PM+MN+PN=PM+CM+CN+PN=PM+AM+BN+PN=PA+PB=2PA=10cm，
∴PA=5cm．
故选A．
∴AM=CM，CN=BN，PA=PB，
∵△PMN的周长为10cm，
即PM+MN+PN=PM+CM+CN+PN=PM+AM+BN+PN=PA+PB=2PA=10cm，
∴PA=5cm．
故选A．
点评：此题考查了切线长定理．此题难度不大，解题的关键是注意数形结合思想的应用．
练习册系列答案
备战中考寒假系列答案
相关题目
5、如图，已知PA、PB切⊙O于点A、B，OP交AB于C，则图中能用字母表示的直角共有（ ）个．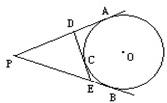
6、如图：PA、PB切⊙O于A、B，过点C的切线交PA、PB于D、E，PA=8cm，则△PDE的周长为
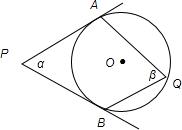22、如图P是⊙O外一点，PA、PB切⊙O于点A、B，Q是优弧AB上的一点，设∠APB=α，∠AQB=β，请探索α与β的关系并证明．
如图，PA、PB切⊙O于点A、B，PA=10，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长是（ ）
如图，PA、PB切⊙O于A、B两点，C为优