题目内容
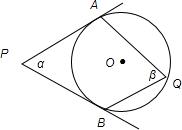22、如图P是⊙O外一点，PA、PB切⊙O于点A、B，Q是优弧AB上的一点，设∠APB=α，∠AQB=β，请探索α与β的关系并证明．分析：连接AO、BO，由PA、PB切⊙O于点A、B得∠PAO=∠PBO=90°，进而可得∠P+∠AOB=180°，由圆周角定理知，∠AOB=2∠Q，所以∠P+2∠Q=180°．
解答：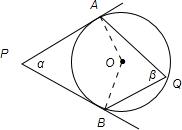
解：因为α+2β=180，
连接AO、BO，∠AOB=2∠Q=2β，
∵PA、PB切⊙O于点A、B，
∴∠PAO=∠PBO=90°，
∴在四边形APBO中有∠AOB+∠P+90°+90°=360°，
∴∠P+∠AOB=180°即α+2β=180°．
解：因为α+2β=180，连接AO、BO，∠AOB=2∠Q=2β，
∵PA、PB切⊙O于点A、B，
∴∠PAO=∠PBO=90°，
∴在四边形APBO中有∠AOB+∠P+90°+90°=360°，
∴∠P+∠AOB=180°即α+2β=180°．
点评：本题利用了切线的性质，圆周角定理，四边形的内角和为360度求解．
练习册系列答案
相关题目
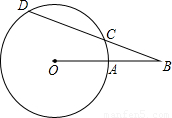
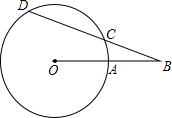如图B是⊙O外一点，BO交⊙O于点A，BCD是⊙O的割线，若BA=3，BC=4，BD=5，则⊙O的半径为
