题目内容
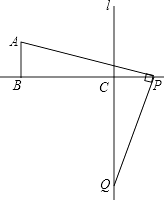
【题目】如图,AB=2,BC=5,AB⊥BC于B,l⊥BC于C,点P自点B开始沿射线BC移动,过点P作PQ⊥PA交直线l于点Q. 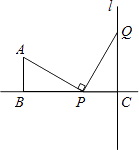
(1)求证:∠A=∠QPC;
(2)当点P运动到何处时,PA=PQ?并说明理由.
【答案】
(1)证明:∵PQ⊥AP,
∴∠ABP=90°
∴∠APB+∠QPC=90°,
∵AB⊥BC于点B,
∴∠A+∠APB=90°,
∴∠A=∠QPC;
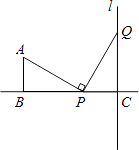
(2)解:当P运动到离C处距离为2时,PA=PQ,
证明:当PC=2时,PC=AB,
在△ABP与△PCQ中,
∵ 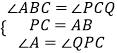 ,
,
∴△ABP≌△PCQ(ASA),
∴PA=PQ;
同理,BP=7时,PC=2也符合,
所以,点P运动到与点C距离为2时,PA=PQ
【解析】(1)根据直角三角形的两内角互余以及∠A+∠APB=90°,根据同角的余角相等,即可证得;(2)P运动到离C处距离为2时,PA=PQ,此时易证△ABP≌△PCQ,即可证得.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目