题目内容
如图,正比例函数y=2x与反比例函数y=| k | x |
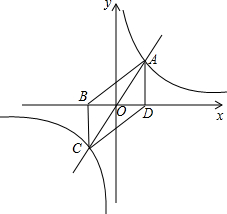 点A作AD垂直x轴,垂足为D,过点C作CB垂直x轴,垂足为B,连接AB和CD.已知点A的横坐标为2.
点A作AD垂直x轴,垂足为D,过点C作CB垂直x轴,垂足为B,连接AB和CD.已知点A的横坐标为2.(1)求k的值;
(2)求证:四边形ABCD是平行四边形;
(3)P、Q两点是坐标轴上的动点(P为正半轴上的点,Q为负半轴上的点),当以A、C、P、Q四点为顶点的四边形是矩形时,求P、Q两点的坐标.
分析:(1)把点A的横坐标代入正比例函数解析式可得点A的纵坐标,把点A的坐标代入反比例函数解析式即可求得k的值;
(2)易得四边形ABCD的对角线互相平分,那么是平行四边形;
(3)若以AC为边得到的矩形,P,Q两点不在坐标轴上;以AC为对角线得到的矩形,可以AC为直径画一个圆,看圆与坐标轴的交点即可.
(2)易得四边形ABCD的对角线互相平分,那么是平行四边形;
(3)若以AC为边得到的矩形,P,Q两点不在坐标轴上;以AC为对角线得到的矩形,可以AC为直径画一个圆,看圆与坐标轴的交点即可.
解答: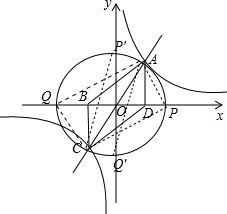 解:(1)当x=2时,由y=2x得y=4,
解:(1)当x=2时,由y=2x得y=4,
∴k=8(4分)
(2)∵A、O、C在一条直线上,A,C在反比例函数和正比例函数的交点处,
∴点A和点C关于点O中心对称,
∴AO=OC,BO=OD,
∴四边形ABCD是平行四边形(或者解方程组y=2x和y=
,求得C点的坐标为(-2,-4)也可)(4分)
(3)∵以AC为边的四边形是矩形时,点P、Q分别在x轴和y轴上时,此时不可能;
∴只能以AC为矩形的对角线,此时P、Q分别在x轴的正、负半轴上或者在y轴的正、负半轴上.
而AO=
=2
,
∴以O为圆心,2
为半径画圆与坐标轴的交点即为所求的点.P(2
,0),Q(-2
,0)或者P(0,2
),Q(0,-2
).(4分)
 解:(1)当x=2时,由y=2x得y=4,
解:(1)当x=2时,由y=2x得y=4,∴k=8(4分)
(2)∵A、O、C在一条直线上,A,C在反比例函数和正比例函数的交点处,
∴点A和点C关于点O中心对称,
∴AO=OC,BO=OD,
∴四边形ABCD是平行四边形(或者解方程组y=2x和y=
| 8 |
| x |
(3)∵以AC为边的四边形是矩形时,点P、Q分别在x轴和y轴上时,此时不可能;
∴只能以AC为矩形的对角线,此时P、Q分别在x轴的正、负半轴上或者在y轴的正、负半轴上.
而AO=
| 22+42 |
| 5 |
∴以O为圆心,2
| 5 |
| 5 |
| 5 |
| 5 |
| 5 |
点评:用到的知识点为:点在函数解析式上,就适合这个函数解析式;正比例函数和反比例函数的交点关于原点对称;直径所对的圆周角是90°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
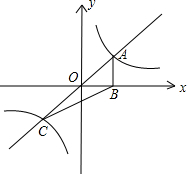 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y=| 1 |
| x |
| A、S=1 | B、S=2 |
| C、S=3 | D、S的值不能确定 |
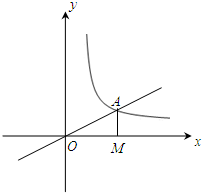 如图,正比例函数
如图,正比例函数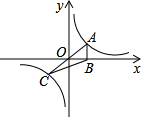 如图,正比例函数y=kx(k>0)与反比例函数y=
如图,正比例函数y=kx(k>0)与反比例函数y= 作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
作x轴的垂线,垂足为M,已知△AOM的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点. 已知:如图,正比例函数y=k1x的图象与反比例函数
已知:如图,正比例函数y=k1x的图象与反比例函数