题目内容
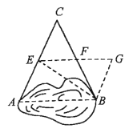
【题目】如图，△ABC中，AB=AC，tanB=
, BC=4,E为BA延长线上一点，⊙E过点C与射线BC的另一交点为F，射线EF与射线AC交于P
（1）求证：AE2=AP·AC
（2）当F点在线段BC上时，设CF=x，△PFC的面积为y，求y与x的函数关系式并写出x的取值范围
（3）当
时求BE
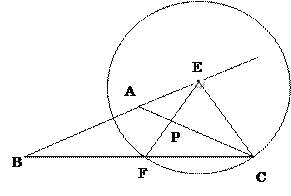
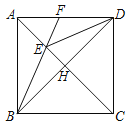
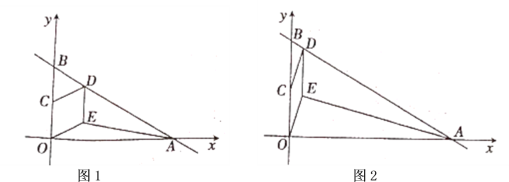
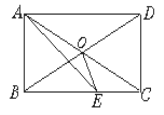
备用图
【答案】（1）见解析；（2）
；（3）
或
.
【解析】分析：
证明△AEP∽△ACE，根据相似三角形的性质得到
，即可证明.
证明△ECB∽△PFC.得到
，求出
，即可得到y与x的函数关系式.
分①
②
两种情况进行讨论.
详解：（1）∵
∴∠B=∠ACB
∵
∴∠EFC=∠ECF
∵
又∵
∴∠BEF=∠ACE
∵
∴△AEP∽△ACE.
∴
∴
（2）∵∠B=∠ACB，∠ECF=∠EFC，
∴△ECB∽△PFC.
∴
∵
∴
.∴
在Rt△BEH中，∵
∴
.
∴
∴
.
∴
（3） ①
∵
∴
∵△AEP∽△ACE.
∴
∴
.
∵ 
∴
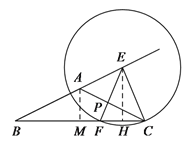
在Rt△ABM中，∵
∴
∴
∴
②
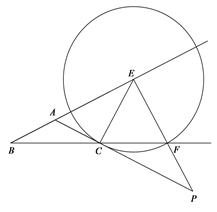
∵∠EFC=∠ECF，
.
又∵
∴∠B =∠FCP.
∴∠P =∠BEC.
∵
∴△AEP∽△ACE，∴
∵∴
∴
∴
.
综上所述,或.
口算题卡加应用题集训系列答案
【题目】为了倡导节约能源，自某日起，我国对居民用电采用阶梯电价，为了使大多数家庭不增加电费支出，事前就需要了解居民全年月平均用电量的分布情况，制订一个合理的方案.某调查人员随机调查了
市
户居民全年月平均用电量(单位：千瓦时)数据如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
得到如下频数分布表：
全年月平均用电量/千时 | 频数 | 频率 |
|
|
|
| ||
| ||
|
| |
|
| |
|
| |
合计 |
|
|
画出频数分布直方图，如下：
(1)补全数分布表和率分布直方图
(2)若是根据数分布表制成扇形统计图，则不低于
千瓦时的部分圆心角的度数为_____________；
(3)若市的阶梯电价方案如表所示，你认为这个阶梯电价方案合理吗?
档次 | 全年月平均用电量/千瓦时 | 电价(元/千瓦时) |
第一档 |
|
|
第二档 |
|
|
第三档 | 大于 |
|
