题目内容
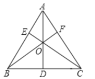
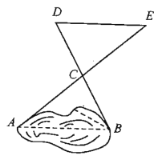
【题目】如图所示,要测量一个沼泽水潭的宽度.现由于不能直接测量,小军是这样操作的:他在平地上选取一点C,该点可以直接到达A与B点,接着他量出AC和BC的距离,并找出AC与BC的中点E、F,连接EF,测量EF的长,于是他便知道了水潭AB的长等于2EF,小军的做法有道理吗?说明理由.你还有比小军更简单的方法吗?
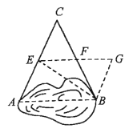
【答案】详见解析
【解析】
仔细阅读题目,分析可知若要说明小军的作法有道理,只需证明AB=2EF即可, 过点B作BG∥AC交EF的延长线于点G,连接BE,利用ASA证明△ECF≌△GBF,得出EF=GF ,CE=BG,再利用SAS证明△AEB≌△GBE得出AB=GE,即可得证.
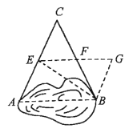
解:小军的作法有道理,理由如下:
过点B作BG∥AC交EF的延长线于点G,连接BE
∵ 点E、F分别是AC、BC的中点
∴ AE=CE, BF=CF
∵ BG∥AC
∴ ∠ECF=∠GBF ,∠AEB=∠GBE (两直线平行,内错角相等)
∵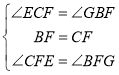
∴ △ECF≌△GBF (两角及其夹边对应相等的两个三角形全等)
∴ EF=GF ,CE=BG (全等三角形的对应边相等)
∵ EF=GF ,EF+GF=EG
∴ EG=2EF
∵ CE=BG, AE=CE
∴ AE=BG
∵ 在△AEB和△GBE中,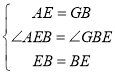
∴ △AEB≌△GBE (两边及其夹角对应相等的两个三角形全等)
∴ AB=GE (全等三角形的对应边相等)
∵ GE=2EF, AB=GE
∴ AB=2EF
故小军的做法是有道理的;
取直接能到达A,B两点的C点,延长BC,AC,使![]() ,
,![]() ,
,
连接DE,
在△ABC和△EDC中,
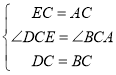
则![]() ,所以
,所以![]() .
.

练习册系列答案
相关题目