题目内容
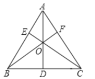
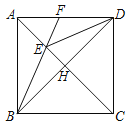
【题目】已知:如图,边长为1的正方形ABCD中,AC 、DB交于点H.DE平分∠ADB,交AC于点E.联结BE并延长,交边AD于点F.
(1)求证:DC=EC;
(2)求△EAF的面积.
![]()
【答案】(1)答案见解析;(2)![]()
【解析】试题分析:(1)根据正方形的性质可得∠ADH=∠HDC=∠DCH=∠DAE=45°,由DE平分∠ADB,可得∠ADE=∠EDH,再由∠DAE+∠ADE=∠DEC,∠EDH+∠HDC=∠EDC,所以∠EDC=∠DEC,即可得DC=EC;(2)根据(1)的结论和勾股定理即可求得AC=![]() , E=
, E= ![]() -1,在Rt△BHC中,求得BH=
-1,在Rt△BHC中,求得BH= ![]() ,根据三角形的面积公式即可求得△BEC的面积,再由AD∥BC,可得△AFE∽△CBE,根据相似三角形面积的比等于相似比的平方即可求得△EAF的面积.
,根据三角形的面积公式即可求得△BEC的面积,再由AD∥BC,可得△AFE∽△CBE,根据相似三角形面积的比等于相似比的平方即可求得△EAF的面积.
试题解析:
(1)∵正方形ABCD,
∴DC=BC=BA=AD,∠BAD=∠ADC=∠DCB=∠CBA=90°,AH=DH=CH=BH,AC⊥BD,
∴∠ADH=∠HDC=∠DCH=∠DAE=45°.
又∵DE平分∠ADB,
∴∠ADE=∠EDH,
∵∠DAE+∠ADE=∠DEC,∠EDH+∠HDC=∠EDC,
∴∠EDC=∠DEC,
∴DC=EC;
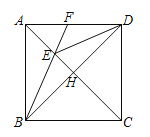
(2)∵正方形ABCD,
∴AD∥BC
,∴△AFE∽△CBE∴![]() ;
;
∵AB=BC=DC=EC=1,AC= ![]() ,
,
∴AE= ![]() ,
,
Rt△BHC中,BH= ![]() BC=
BC= ![]() ,
,
∴在△BEC中,BH⊥EC,![]() ,
,
∴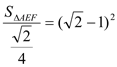 ,
,
∴![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.