题目内容
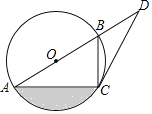
【题目】如图,在![]() 中,
中,![]() , 点
, 点![]() 是边
是边![]() 上一动点(不与
上一动点(不与![]() 重合),
重合),![]() =
=![]()
![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,则线段
,则线段![]() 的最大值为___.
的最大值为___.

【答案】![]()
【解析】
作AG⊥BC于G,如图,根据等腰三角形的性质得BG=CG,再利用余弦的定义计算出BG=8,则BC=2BG=16,设BD=x,则CD=16-x,证明△ABD∽△DCE,利用相似比可表示出![]() ,然后利用二次函数的性质求CE的最大值.
,然后利用二次函数的性质求CE的最大值.
作AG⊥BC于G,如图,

∵AB=AC,
∴BG=CG,
∵∠ADE=∠B=α,
∴cosB=cosα=![]() ,
,
∴BG=![]() ×10=8,
×10=8,
∴BC=2BG=16,
设BD=x,则CD=16-x,
∵∠ADC=∠B+∠BAD,即α+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
而∠B=∠C,
∴△ABD∽△DCE,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
当x=8时,CE最大,最大值为6.4.

【题目】一中和二中举行数学知识竞赛,参赛学生的竞赛得分统计结果如下表:
学校 | 参赛人数 | 平均数 | 中位数 | 方差 |
一中 | 45 | 83 | 86 | 82 |
二中 | 45 | 83 | 84 | 135 |
某同学分析上表后得到如下结论:.
①一中和二中学生的平均成绩相同;
②一中优秀的人数多于二中优秀的人数(竞赛得分![]() 85分为优秀);
85分为优秀);
③二中成绩的波动比一中小.
上述结论中正确的是___________. (填写所有正确结论的序号)
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数y=ax2+bx+C的最大值为6;③抛物线的对称轴是x=![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A.1个B.2个C.3个D.4个
【题目】某水产养殖户进行小龙虾养殖. 已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,日销售量![]() 与时间第
与时间第![]() 天之间的函数关系式为
天之间的函数关系式为![]() (
(![]() ,
,![]() 为整数),销售单价
为整数),销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间满足一次函数关系如下表:
天之间满足一次函数关系如下表:
时间第 | 1 | 2 | 3 | … | 80 |
销售单价 | 49. 5 | 49 | 48. 5 | … | 10 |
(1)写出销售单价![]() (元/
(元/![]() )与时间第
)与时间第![]() 天之间的函数关系式;
天之间的函数关系式;
(2)在整个销售旺季的80天里,哪一天的日销售利润最大?最大利润是多少?