Question

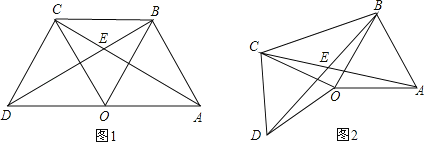
【题目】已知点C是线段AB上一点，在线段AB的同侧作△CAD和△CBE，直线BD和AE相交于点F，CA=CD，CB=CE，∠ACD=∠BCE。

（1）如图①，若∠ACD=600，则∠AFB=___________；若∠ACD=，则∠AFB=___________。

（2）如图②，将图①中的△CAD绕点C顺时针旋转任意角度（交点F至少在BD、AE中的一条线段上），试探究∠AFB与的数量关系，并说明理由。

Answer 1

【答案】（1）120°；180°；(2) ∠AFB=180°.

【解析】

（1）由∠ACD=∠BCE得到∠ACE=∠DCB，通过证明△ACE≌△DCB得∠CBD=∠CEA，由三角形内角和定理得到结论∠AFB=180°-，代入∠ACD=60°即可求解.

（2）由∠ACD=∠BCE得到∠ACE=∠DCB，再由三角形的内角和定理得∠CAE=∠CDB，从而得出∠DFA=∠ACD，得到结论∠AFB=180°-．

（1）∵∠ACD=∠BCE=，则∠ACD+∠DCE=∠BCE+∠DCE，

即∠ACE=∠DCB.

在△ACE和△DCB中，

则△ACE≌△DCB(SAS).

则∠CBD=∠CEA，由三角形内角和知∠EFB=∠ECB=.

∠AFB=180°∠EFB=180°.

故当∠ACD=60°，∠AFB=180°60°=120°

故答案为：120°；180°；

(2)∵∠ACD=∠BCE，

∴∠ACD+∠DCE=∠BCE+∠DCE.

∴∠ACE=∠DCB.

∴∠CAE=∠CDB.

∴∠DFA=∠ACD.

∴∠AFB=180°∠DFA=180°∠ACD=180°.