题目内容
【题目】如图,将边长分别为1、2、3、4……19、20的正方形置于直角坐标系第一象限,如图中方式叠放,则按图示规律排列的所有阴影部分的面积之和为.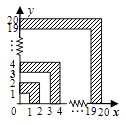
【答案】210
【解析】
图中阴影部分的面积为:
(22-1)+(42-32)+…+(202-192)
=(2+1)(2-1)+(4+3)(4-3)+…+(20+19)(20-19)
=1+2+3+4+…+19+20
=210.
观察图可知:第一个阴影部分的面积等于第二个正方形的面积减去第一个正方形的面积;第二个阴影部分的面积等于第四个正方形的面积减去第三个正方形的面积;第三个阴影部分的面积等于第六个正方形的面积减去第五个正方形的面积;由此类推,最后一个阴影部分的面积就应该等于最后一个正方形的面积减去倒数第二个图形的面积;从而列出算式(22-1)+(42-32)+…+(202-192),利用平方差公式分解因式,然后计算括号里面,再计算括号外面的顺序算出结果即可。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目