题目内容
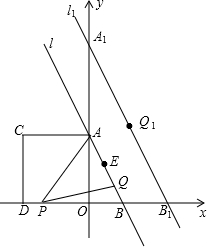 (2013•金平区模拟)如图,直线l:y=-2x+4交y轴于A点,交x轴于B点,四边形OACD为正方形,点P从D点开始沿x轴向点O以每秒2个单位的速度移动,点Q从点B开始沿BA向点A以每秒
(2013•金平区模拟)如图,直线l:y=-2x+4交y轴于A点,交x轴于B点,四边形OACD为正方形,点P从D点开始沿x轴向点O以每秒2个单位的速度移动,点Q从点B开始沿BA向点A以每秒| 5 |
(1)设△PAQ的面积等于S,运动时间为t秒,当0<t<2时,求S与t之间的函数关系;
(2)当点Q移到AB的中点E时,P点停止移动.直线l向右平移m个单位,得到直线l1.
如图,直线l1交y轴于A1点,交x轴于B1点,Q1为A1B1的中点.△PAQ1的面积S1是否与m的值有关?请说明你的理由.
分析:(1)先求出A和B点的坐标,当0<t<2时,DP=2t,BQ=
t,在Rt△AOB中,求出AB的长度,作QF⊥OB于F,结合题干条件,证明△QFB∽△AOB,用t表示出QF,S=S△PBA-S△PBQ,进而求出S与t之间的函数关系;
(2)方法一、设OD的中点为G,则当点Q移到AB的中点E时,P点与G点重合,△PAQ1的面积即为△GAQ1,利用题干条件求出△GAQ1的面积是个常数即可;
方法二:作Q1M⊥OB1于M,根据题干条件用m分别表示出OB1、OA1、MB1、OM,再根据S1=S△AOB+S梯形AOMQ1-S△GMQ1,求出S1是一个常数即可;
| 5 |
(2)方法一、设OD的中点为G,则当点Q移到AB的中点E时,P点与G点重合,△PAQ1的面积即为△GAQ1,利用题干条件求出△GAQ1的面积是个常数即可;
方法二:作Q1M⊥OB1于M,根据题干条件用m分别表示出OB1、OA1、MB1、OM,再根据S1=S△AOB+S梯形AOMQ1-S△GMQ1,求出S1是一个常数即可;
解答: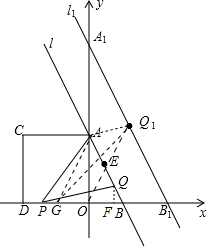 解:(1)∵直线l:y=-2x+4交y轴于A点,交x轴于B点,
解:(1)∵直线l:y=-2x+4交y轴于A点,交x轴于B点,
∴A(0,4),B(2,0)
∴OA=4,OB=2,
依题意,得OD=OA=4,
当0<t<2时,DP=2t,BQ=
t,
∴PB=DB-DP=6-2t,
在Rt△AOB中,AB=
=2
,
作QF⊥OB于F,
∵AO⊥OB,
∴AO∥QF,
∴△QFB∽△AOB,
∴
=
,
∴QF=
×AO=2t,
S=
PB•OA-
PB•QF=
PB(OA-QF),
∴S=S△PBA-S△PBQ=
×(6-2t)×(4-2t),
∴S=2t2-10t+12.
(2)△PAQ1的面积S1与m的值无关,S1=4.理由如下:
设OD的中点为G,则当点Q移到AB的中点E时,P点与G点重合,
△PAQ1的面积即为△GAQ1.
解法一:∵Q1为A1B1的中点,
∴OQ1=B1Q1,
∴∠B1OQ1=∠OB1Q1,
∵l∥l1,
∴∠ABO=∠OB1Q1,
∵OG=OB=2,AO⊥OB,
∴AG=AB,
∴∠ABO=∠AGO,
∴∠B1OQ1=∠AGO,
∴AG∥OQ1,
∴△PAQ1的面积S1=S△AGO=
×OG•OA=4,
∴S1的值为4,与m的值无关.
解法二:依题意,得OB1=2+m,
∵l∥l1,
∴△A10B1∽△AOB,
∴
=
,
∴OA1=
×OB1=
×(2+m)=4+2m,
如图,作Q1M⊥OB1于M,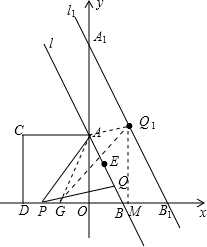
∵AO⊥OB,
∴AO∥Q1M,
∵Q1为A1B1的中点,
∴MB1=
OB1=1+
m,Q1M=
OA1=2+m,
∴OM=OB1-B1M=1+
m,
∴S1=S△AOB+S梯形AOMQ1-S△GMQ1
=
×2×4+
(4+2+m)(
+m)-
(2+1+
m)(2+m)
=4
∴S1的值为4,与m的值无关.
 解:(1)∵直线l:y=-2x+4交y轴于A点,交x轴于B点,
解:(1)∵直线l:y=-2x+4交y轴于A点,交x轴于B点,∴A(0,4),B(2,0)
∴OA=4,OB=2,
依题意,得OD=OA=4,
当0<t<2时,DP=2t,BQ=
| 5 |
∴PB=DB-DP=6-2t,
在Rt△AOB中,AB=
| OA2+OB2 |
| 5 |
作QF⊥OB于F,
∵AO⊥OB,
∴AO∥QF,
∴△QFB∽△AOB,
∴
| QF |
| AO |
| BQ |
| AB |
∴QF=
| BQ |
| AB |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S=S△PBA-S△PBQ=
| 1 |
| 2 |
∴S=2t2-10t+12.
(2)△PAQ1的面积S1与m的值无关,S1=4.理由如下:
设OD的中点为G,则当点Q移到AB的中点E时,P点与G点重合,
△PAQ1的面积即为△GAQ1.
解法一:∵Q1为A1B1的中点,
∴OQ1=B1Q1,
∴∠B1OQ1=∠OB1Q1,
∵l∥l1,
∴∠ABO=∠OB1Q1,
∵OG=OB=2,AO⊥OB,
∴AG=AB,
∴∠ABO=∠AGO,
∴∠B1OQ1=∠AGO,
∴AG∥OQ1,
∴△PAQ1的面积S1=S△AGO=
| 1 |
| 2 |
∴S1的值为4,与m的值无关.
解法二:依题意,得OB1=2+m,
∵l∥l1,
∴△A10B1∽△AOB,
∴
| OA1 |
| OB1 |
| OA |
| OB |
∴OA1=
| OA |
| OB |
| 4 |
| 2 |
如图,作Q1M⊥OB1于M,

∵AO⊥OB,
∴AO∥Q1M,
∵Q1为A1B1的中点,
∴MB1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OM=OB1-B1M=1+
| 1 |
| 2 |
∴S1=S△AOB+S梯形AOMQ1-S△GMQ1
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4
∴S1的值为4,与m的值无关.
点评:本题主要考查一次函数的综合题的知识,解答本题的关键是熟练掌握相似三角形的性质以及分割法求三角形的面积,此题难度较大,特别是第二问证明S1的面积是一个常数,但是解答此问的时候也不止一种方法,希望同学们根据自己喜欢的方法解答即可.

练习册系列答案
相关题目
 (2013•金平区模拟)木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的根据是( )
(2013•金平区模拟)木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的根据是( ) (2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是
(2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是