题目内容
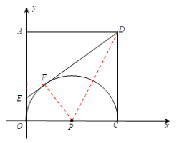
【题目】如图，边长为4的正方形AOCD的顶点A、C分别在y轴和x轴上，点P的坐标为（2，0），以点P为圆心，OP的长为半径向正方形内部作一半圆，交线段DF于点F，线段DF的延长线交y轴于点E，DF=DC.
（1）求证：DF是半圆P的切线；
（2）求线段DF所在直线的解析式；
【答案】（1）证明见解析；（2）直线DF的解析式为
【解析】（1）首先利用SSS，得出△PDF≌△PDC，即可得出答案；
（2）由题意得：在Rt△ADE中，DE2=AD2+AE2，进而得出E点坐标，再利用待定系数法求一次函数解析式.
（1）证明：连接PD、PF.
∵正方形AOCD的边长为4，而P的坐标为（2，0），
∴OP = 2，即P为BC的中点，有
， 又DF= DC，PD = PD，
∴△PDF≌△PDC，
得∠PFD = ∠PCD，而
，
，故DF是半圆P的切线.
（2）解：据题意，显然有EO切圆P于点O，
而EF切圆P于点F，则有EO = EF.若设EO = x，则
，
，因而在
中，
，
，
解得
即E点坐标为（0，1）.又点D为（4，4），
设直线DF的解析式为
，那么有
，解得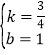
.
∴直线DF的解析式为
练习册系列答案
阅读快车系列答案
相关题目
