题目内容
 已知△ABC,D是BC的中点,将三角板中的90°角的顶点绕D点在△ABC内旋转,角的两边分别与AB、AC交于E、F,且点E、F不与A、B、C三点重合.
已知△ABC,D是BC的中点,将三角板中的90°角的顶点绕D点在△ABC内旋转,角的两边分别与AB、AC交于E、F,且点E、F不与A、B、C三点重合.(1)如果∠A=90°,观察并探索,当E、F点位置变化时,BE、EF、CF三条线段中有否有一条线段始终最长.请指出,并给予证明.
(2)请分别∠A>90°、∠A<90°两种情况考察BE、EF、CF三条线段中有否有一条线段始终最长.如果有请,指出最长的线段,但不需证明;如果没有,请画草图举出反例.
分析:(1)根据旋转的性质,推理得出三角形全等,根据全等的性质及直角三角形斜边最大即可推理得出,
(2)根据(1)中结论即可画图反例图示.
(2)根据(1)中结论即可画图反例图示.
解答: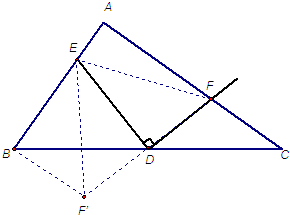 解:(1)答:线段EF始终最大,证明如下:
解:(1)答:线段EF始终最大,证明如下:
将△FDC绕点D顺时针方向旋转180°,如图,
∵D是BC的中点,
∴点C旋转后与点B重合,△FDC≌△F′DB,∠FCD=F′BD,DF=DF′,FC=F′B,
连接EF、EF’,
在△EDF和△EDF’中,
∵∠EDF=90°=∠EDF,ED=ED,FD=F′D,
∴△FDE≌△F′DE,
∴EF=EF’,
在△EBF’中,∠EBF’=∠EBD+∠F’BD=∠EBD+∠FCD=180°-∠A=90°,
EF’是Rt△EBF′斜边EF′>EB,EF′>BF′,
∴BE、EF、CF三条线段中,EF的长度始终最大,
(2)当∠A<90°,BE、EF、CF三条线段中,EF始终最长,(原因∠EBF’>180°,
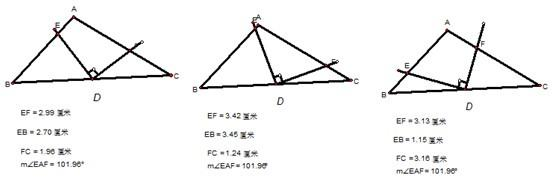
当∠A>90°,BE、EF、CF三条线段中,不存在始终最长的线段,反例如图:
 解:(1)答:线段EF始终最大,证明如下:
解:(1)答:线段EF始终最大,证明如下:将△FDC绕点D顺时针方向旋转180°,如图,
∵D是BC的中点,
∴点C旋转后与点B重合,△FDC≌△F′DB,∠FCD=F′BD,DF=DF′,FC=F′B,
连接EF、EF’,
在△EDF和△EDF’中,
∵∠EDF=90°=∠EDF,ED=ED,FD=F′D,
∴△FDE≌△F′DE,
∴EF=EF’,
在△EBF’中,∠EBF’=∠EBD+∠F’BD=∠EBD+∠FCD=180°-∠A=90°,
EF’是Rt△EBF′斜边EF′>EB,EF′>BF′,
∴BE、EF、CF三条线段中,EF的长度始终最大,
(2)当∠A<90°,BE、EF、CF三条线段中,EF始终最长,(原因∠EBF’>180°,
当∠A>90°,BE、EF、CF三条线段中,不存在始终最长的线段,反例如图:

点评:本题主要考查了旋转的性质及三角形全等证明及性质,同时考查了三角形三边关系,难度较大.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知△ABC的周长是24,且AB=AC,又AD⊥BC,D为垂足,若△ABD的周长是20,则AD的长为( )
| A、6 | B、8 | C、10 | D、12 |
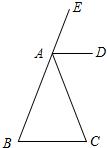 26、如图,已知△ABC,∠CAE是△ABC的外角,在下列三项中:①AB=AC;②AD平分∠CAE;③AD∥BC.选择两项为题设,另一项为结论,组成一个真命题,并证明.
26、如图,已知△ABC,∠CAE是△ABC的外角,在下列三项中:①AB=AC;②AD平分∠CAE;③AD∥BC.选择两项为题设,另一项为结论,组成一个真命题,并证明.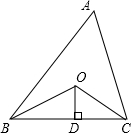 如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是
如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,△ABC的面积是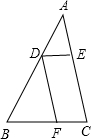 已知△ABC,D是边AB上的一点,DE∥BC交AC于点E,DF∥AC交BC于点F,若△ADE、△DBF的面积分别为1和2,则四边形DECF的面积为( )
已知△ABC,D是边AB上的一点,DE∥BC交AC于点E,DF∥AC交BC于点F,若△ADE、△DBF的面积分别为1和2,则四边形DECF的面积为( )