题目内容
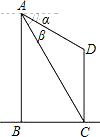如图，两建筑物的水平距离BC为24米，从点A测得点D的俯角α=30°，测得点C的俯角β=60°，求AB和CD两座建筑物的高．（结果保留根号）
分析：在直角△ABC和直角△ADE中，根据AE可以求得AB、DE的长，根据AB、DE可以求得CD的长，即可解题．
解答：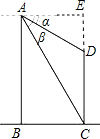
解：延长CD至E，作AE⊥CE，
则
=tanβ，
∴AB=
BC=24
米，
DE=AE•tanα=8
米，
∴CD=AB-DE=16
米．
解：延长CD至E，作AE⊥CE，则
| AB |
| BC |
∴AB=
| 3 |
| 3 |
DE=AE•tanα=8
| 3 |
∴CD=AB-DE=16
| 3 |
点评：本题考查了直角三角形中三角函数的运用，特殊角的三角函数值，本题中求DE的长是解题的关键．
练习册系列答案
相关题目
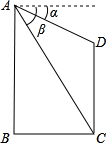如图，两建筑物的水平距离BC为27米，从点A测得点D的俯角α=30°，测得点C的俯角β=60°，求AB和CD两建筑物的高．
5、如图，两建筑物的水平距离为30m，从A点测得D点的俯角为75°，测得C点的俯角为35°，则较低建筑物CD的高为（ ）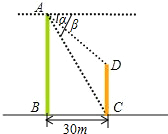
（1997•广西）如图，两建筑物的水平距离为30米，从A点测得D点的俯角α为45°，测得C点的俯角β为60°，求这两个建筑物AB、CD的高（结果保留根号）．