题目内容
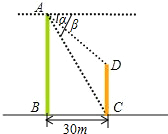 (1997•广西)如图,两建筑物的水平距离为30米,从A点测得D点的俯角α为45°,测得C点的俯角β为60°,求这两个建筑物AB、CD的高(结果保留根号).
(1997•广西)如图,两建筑物的水平距离为30米,从A点测得D点的俯角α为45°,测得C点的俯角β为60°,求这两个建筑物AB、CD的高(结果保留根号).分析:过D作DE⊥AB,垂足为E,则∠ADE=α=45°,继而可求出AE,在Rt△ABC中求出AB,继而可得出AB、CD的高.
解答:解:过D作DE⊥AB,垂足为E,
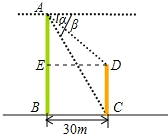
在Rt△ADE中,∠ADE=45°,
∴AE=DE=BC=30米,
在Rt△ABC中,∠ACB=60°,
则AB=BCtan60°=30
米,
故CD=(30
-30)米.
答:两个建筑物AB、CD的高分别为30
米、(30
-30)米.

在Rt△ADE中,∠ADE=45°,
∴AE=DE=BC=30米,
在Rt△ABC中,∠ACB=60°,
则AB=BCtan60°=30
| 3 |
故CD=(30
| 3 |
答:两个建筑物AB、CD的高分别为30
| 3 |
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,然后利用解直角三角形的知识求出各线段的长度.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
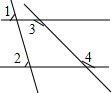 (1997•广西)如图,∠1=∠2,∠3=135°,那么∠4=
(1997•广西)如图,∠1=∠2,∠3=135°,那么∠4=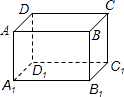 (1997•广西)如图,在长方体中,面ABCD与面
(1997•广西)如图,在长方体中,面ABCD与面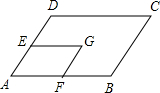 (1997•广西)如图,E、F分别是?ABCD相邻两边的中点,四边形AFGE也是平行四边形,那么S?AFGE:S?ABCD=
(1997•广西)如图,E、F分别是?ABCD相邻两边的中点,四边形AFGE也是平行四边形,那么S?AFGE:S?ABCD=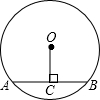 (1997•广西)如图,在半径为5的⊙O中,弦AB的长为6,那么弦心距OC=( )
(1997•广西)如图,在半径为5的⊙O中,弦AB的长为6,那么弦心距OC=( ) (1997•广西)如图,DE∥BC,AB=15,AC=9,BD=4,那么AE=( )
(1997•广西)如图,DE∥BC,AB=15,AC=9,BD=4,那么AE=( )