题目内容
【题目】已知:等边△ABC中,点E为△ABC内一点.
(1)如图1,联结AE、BE并延长分别与BC、CA边交于点D、F。如果∠AEB=120°,求证:△ABD![]() △BCF。
△BCF。
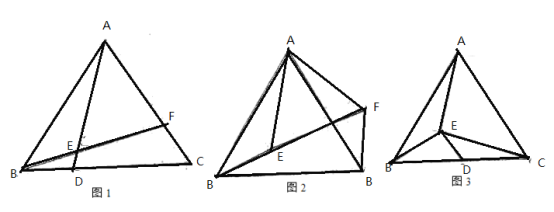
(2)如图2、以AE为一边作等边△AEF,联结BE、CF,求证:BE=CF.
(3)如图3、点D为BC的中点,联结BE、CE,若∠BEC=120°,联结AE、DE,求证:AE=2DE.
【答案】(1)见详解;(2)见详解;(3)见详解.
【解析】
(1)由∠AEB=120°,得到∠BAE+∠ABE=60°,即可得到∠BAE=∠CBF,然后利用ASA证明△ABD≌△BCF即可;
(2)由等边三角形△ABC、△AEF,得到AB=AC,AE=AF,∠BAC=∠EAF=60°,则得到∠BAE=∠CAF,然后证明△ABE≌△ACF,即可得到结论成立;
(3)把△ABE逆时针旋转60°,得到△ACF,连接EF,延长ED至点G,使得ED=DG,连接CG. 由旋转的性质,得△ABE≌△ACF,且△AEF时等边三角形;由∠BEC=120°,得到∠EBD+∠ECD=60°,根据角的等量代换得到∠ECF=∠ECG=60°,然后得到△ECG≌△ECF,得到EG=EF=AE,即可得到AE=2ED.
证明:(1)如图,
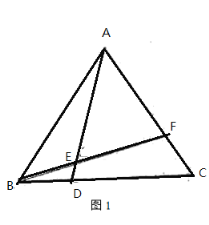
在等边△ABC中,有AB=BC,∠ABC=∠C=60°,
∵∠AEB=120°,
∴∠BED=180°![]() 120°=60°,
120°=60°,
∴∠BAE+∠ABE=60°,
∵∠CBF+∠ABE=∠ABC=60°,
∴∠BAE=∠CBF,
∴△ABD≌△BCF(ASA);
(2)如图,
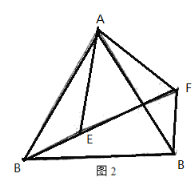
∵△ABC和△AEF是等边三角形,
∴AB=AC,AE=AF,∠BAC=∠EAF=60°,
∴∠BAE+∠EAC=∠EAC+∠CAF=60°,
∴∠BAE=∠CAF,
∴△ABE≌△ACF(SAS),
∴BE=CF;
(3)如图,把△ABE逆时针旋转60°,得到△ACF,连接EF,延长ED至点G,使得ED=DG,连接CG.
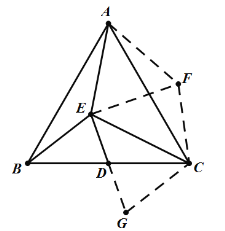
由旋转的性质,得:△ABE≌△ACF,且△AEF时等边三角形,
∴AE=AF=EF,BE=CF,∠ABE=∠ACF,
∵∠BEC=120°,
∴∠EBD+∠ECD=60°,
∵∠EBD+∠ABE=∠ABC=60°,
∴∠ABE=∠ECD=∠ACF,
∴∠ACF+∠ACE=∠ECD+∠ACE=∠ACB=60°,
∴∠ECF=60°.
∵ED=DG,∠BDE=∠CDG,BD=CD,
∴△BDE≌△CDG,
∴BE=CG=CF,∠EBD=GCD,
∴∠GCD+∠ECD=∠EBD+∠ABE=∠ABC=60°,
∴∠ECG=60°,
∴∠ECF=∠ECG=60°,
在△ECG和△ECF中,
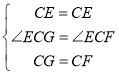 ,
,
∴△ECG≌△ECF,
∴EG=EF=AE,
∵EG=2ED,
∴AE=2ED.