题目内容
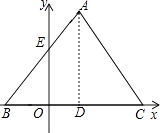
【题目】如图,直线y=﹣
x+8与x轴、y轴分别交于A．B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处，则点M的坐标是（ ）
A. （0,4） B. （0,3） C. （﹣4,0） D. （0,﹣3）
【答案】D
【解析】∵直线y=
x+8与x轴、y轴分别交于点A和点B，
∴y=0时,x=6,则A点坐标为：(6,0)，
x=0时,y=8,则B点坐标为：(0,8)；
∴BO=8，AO=6，
∴AB=
=10，
直线AB沿AM折叠，点B恰好落在x轴上的点C处，
∴AB=AC=10，MB=MC，
∴OC=ACOA=106=4.
设MO=x，则MB=MC=8x，
在Rt△OMC中,OM2+OC2=CM2，
∴x2+42=(8x)2，
解得：x=3，
故M点坐标为：(0,3).
故选B.
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
