题目内容
(1997•河北)已知圆锥的母线长AB=6cm,底面半径OB=2cm,则它的侧面展开扇形的圆心角为
120
120
°.分析:易得圆锥的底面周长,也就是圆锥的侧面展开图的弧长,利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角.
解答:解:∵圆锥的底面半径为2cm,
∴圆锥的底面周长为4π,
设扇形的圆心角为n°,
∴
=4π,
解得n=120.
答:圆锥的侧面展开图中扇形的圆心角为120°.
故答案为:120.
∴圆锥的底面周长为4π,
设扇形的圆心角为n°,
∴
| nπ×6 |
| 180 |
解得n=120.
答:圆锥的侧面展开图中扇形的圆心角为120°.
故答案为:120.
点评:此题主要考查了圆锥的有关计算,用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (1997•河北)已知:如图,DE∥BC,AD=3.6,DB=2.4,AC=7.求EC的长.
(1997•河北)已知:如图,DE∥BC,AD=3.6,DB=2.4,AC=7.求EC的长.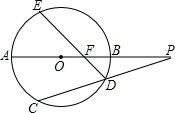 (1997•河北)已知:如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,弧AE=弧AC,ED交AB于点F.求证:PF•PO=PA•PB.
(1997•河北)已知:如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,弧AE=弧AC,ED交AB于点F.求证:PF•PO=PA•PB.