题目内容
【题目】AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
①求证:DC为⊙O切线;
②若ADOC=8,求⊙O半径r.
【答案】证明:①连接OD.
∵OA=OD,
∴∠A=∠ADO.
∵AD∥OC,
∴∠A=∠BOC,∠ADO=∠COD,
∴∠BOC=∠COD.
∵在△OBC与△ODC中,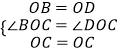 ,
,
∴△OBC≌△ODC(SAS),
∴∠OBC=∠ODC,
又∵BC是⊙O的切线,
∴∠OBC=90°,
∴∠ODC=90°,
∴DC是⊙O的切线;
②解:连接BD.
∵在△ADB与△ODC中, ![]() ,
,
∴△ADB∽△ODC,
∴AD:OD=AB:OC,
∴ADOC=ODAB=r2r=2r2 , 即2r2=8,
故r=2.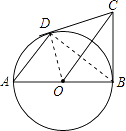
【解析】①连接OD,要证明DC是⊙O的切线,只要证明∠ODC=90°即可.根据题意,可证△OCD≌△OCB,即可得∠CDO=∠CBO=90°,由此可证DC是⊙O的切线;②连接BD,OD.先根据两角对应相等的两三角形相似证明△ADB∽△ODC,再根据相似三角形对应边成比例即可得到r的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






