题目内容
如图,在平面直角坐标系中,反比例函数 (x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6) .
(x>0)的图象和矩形ABCD的第一象限,AD平行于x轴,且AB=2,AD=4,点A的坐标为(2,6) .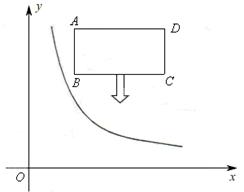
(1)直接写出B、C、D三点的坐标;
(2)若将矩形向下平移,矩形的两个顶点恰好同时落在反比例函数的图象上,猜想这是哪两个点,并求矩形的平移距离和反比例函数的解析式.
解:(1)B(2,4),C(6,4),D(6,6)。
(2)猜想矩形的A、C两顶点恰好同时落在反比例函数的图象上。
如图,矩形ABCD向下平移后得到矩形 ,
,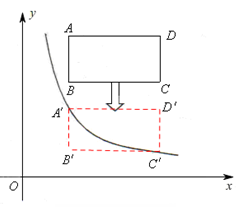
设平移距离为a,则A′(2,6-a),C′(6,4-a)。
∵点A′,点C′在 的图象上,
的图象上,
∴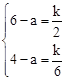 , 解得
, 解得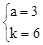 。
。
∴矩形的平移距离为3,反比例函数的解析式为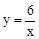 。
。
解析试题分析:(1)根据矩形的对边平行且相等的性质即可得到B、C、D三点的坐标。
(2)从矩形的平移过程发现只有A、C两点能同时在双曲线上,设平移距离为a,得到A′(2,6-a),C′(6,4-a),代入 中,得到关于a、k的方程组从而求得a、k的值,从而得到矩形的平移距离和反比例函数的解析式。
中,得到关于a、k的方程组从而求得a、k的值,从而得到矩形的平移距离和反比例函数的解析式。

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
的函数图象经过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数图象的一个公共点.
 的图象与反比例函数
的图象与反比例函数 的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.
的图象的两个交点是A(-2,-4),C(4,n),与y轴交于点B,与x轴交于点D.
 与
与 ,如果存在函数
,如果存在函数 (
(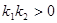 )则称函数
)则称函数 ,并且其中一个函数满足:当
,并且其中一个函数满足:当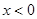 时,
时, 随
随 的增大而增大.
的增大而增大.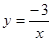 和
和 的中和函数
的中和函数 的图象和函数
的图象和函数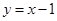 的图象相交于两点,试求当
的图象相交于两点,试求当 在反比例函数
在反比例函数 的图象上,它关于
的图象上,它关于 轴的对称点在一次函数
轴的对称点在一次函数 的图象上,求此反比例函数的解析式.
的图象上,求此反比例函数的解析式.
 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数 的图象经过点M,N.
的图象经过点M,N.

