题目内容
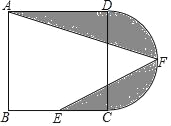
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),在
重合),在![]() 同侧分别作等边
同侧分别作等边![]() 和等边
和等边![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .下列五个结论:①
.下列五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④DE=DP;⑤
;④DE=DP;⑤![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
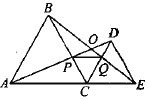
A.2个B.3个C.4个D.5个
【答案】C
【解析】
①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE;
②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;
③根据②△CQB≌△CPA(ASA),可知③正确;
④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;
⑤由BC∥DE,得到∠CBE=∠BED,由∠CBE=∠DAE,得到∠AOB=∠OAE+∠AEO=60°.
解:∵等边△ABC和等边△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
在△ACD与△BCE中,
 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE, 故①正确,
∵△ACD≌△BCE,
∴∠CBE=∠DAC,
又∵∠ACB=∠DCE=60°,
∴∠BCD=60°,即∠ACP=∠BCQ,
又∵AC=BC,
∴△CQB≌△CPA(ASA),
∴CP=CQ,
又∵∠PCQ=60°可知△PCQ为等边三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE, 故②正确,
∵△CQB≌△CPA,
∴AP=BQ, 故③正确,
∵AD=BE,AP=BQ,
∴AD-AP=BE-BQ,
即DP=QE,
∵∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,故④错误;
∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AOB=∠OAE+∠AEO=60°,故⑤正确;
综上所述,正确的有4个,
故选:C.