Question

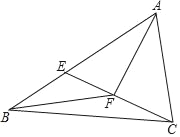
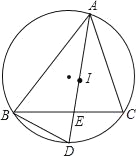
【题目】如图，点I是△ABC的内心，AI的延长线和△ABC的外接圆相交于点D，与BC相交于点E．

（1）求证：DI=DB；

（2）若AE=6cm，ED=4cm，求线段DI的长．

Answer 1

【答案】（1）见解析；（2）2cm.

【解析】

（1）要证明ID=BD，只要求得∠BID=∠IBD即可；

（2）根据相似三角形的判定得出△BDE∽△ABD，进而利用相似三角形的性质解答即可.

（1）证明：连接BI．

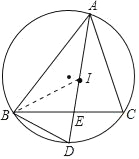
∵点I是△ABC的内心，

∴∠BAI=∠CAI，∠ABI=∠CBI．

又∵∠DBI=∠CBI+∠DBC，∠DIB=∠ABI+∠BAI，

∠DBC=∠DAC=∠BAI，

∴∠DBI=∠DIB，

∴DI=DB．

（2）∵∠DBC=∠DAC=∠BAI，∠ADB=∠BDA，

∴△BDE∽△ABD，

∴，

即BD2=DEAD=DE（AE+DE）=4×（6+4）=40，

DI=BD=（cm）．