题目内容
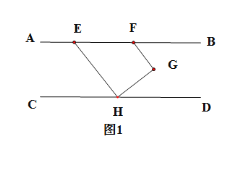
【题目】如图AB∥CD,点H在CD上,点E、F在AB上,点G在AB、CD之间,连接FG、GH、HE,HG⊥HE,垂足为H,FG⊥HG,垂足为G.
(1)求证:∠EHC+∠GFE=180°.
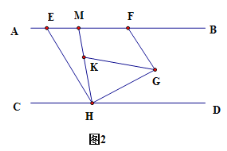
(2)如图2,HM平分∠CHG,交AB于点M,GK平分∠FGH,交HM于点K,求证:∠GHD=2∠EHM.
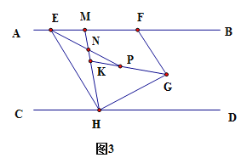
(3)如图3,EP平分∠FEH,交HM于点N,交GK于点P,若∠BFG=50°,求∠NPK的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)20°
【解析】
(1)根据HG⊥HE,FG⊥HG可证明FG∥EH,从而得∠GFE+∠HEF=180°,再根据AB∥CD可得∠BEH=∠CHE,进而可得结论;
(2)设∠EHM=x,根据MH是∠CHG的平分线可得∠MHG=90°-x,∠EHC=90°-2x,根据平行线的性质得∠HMB=90°-x,从而得∠HMB=∠MHG,再由平行线的性质得∠BMH+∠DHM=180°,从而可得结论;
(3)分别延长FG,GK,交CD于R,交HE于S,由AB∥CD得∠HRG=50°,由FG⊥HG得∠GHR=40°,由MH平分∠CHG得∠CHE=50°,由AB∥CD得∠MEH=∠CHE=50°,可得∠SEP=25°,最后由三角形的外角可得结论.
(1)∵HG⊥HE,FG⊥HG
∴FG∥EH,
∴∠GFE+∠HEF=180°,
∵AB∥CD
∴∠BEH=∠CHE
∴∠EHC+∠GFE=180°
(2)设∠EHM=x,
∵HG⊥HE,
∴∠GHK=90°-x,
∵MH平分∠CHG,
∴∠EHC=90°-2x,
∵AB∥CD
∴∠HMB=90°-x,
∴∠HMB=∠MHG=90°-x,
∵AB∥CD,
∴∠BMH+∠DHM=180°,即∠BMH+∠GHM+∠GHD =180°,
∴90°-x+90°-x+∠GHD =180°,解得,∠GHD =2x,
∴∠GHD=2∠EHM;
(3)延长FG,GK,交CD于R,交HE于S,如图,
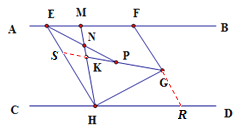
∵AB∥CD,∠BFG=50°
∴∠HRG=50°
∵FG⊥HG,
∴∠GHR=40°,
∵HG⊥HE,
∴∠EHG=90°,
∴∠CHE=180°-90°-40°=50°,
∵AB∥CD,
∴∠FEH=∠CHE=50°,
∵EP是∠HEF的平分线,
∴∠SEP=![]() ∠FEH=25°,
∠FEH=25°,
∵GH平分∠HGF,
∴∠HGS=![]() ∠HGF=45°,
∠HGF=45°,
∴∠HSG=45°,
∵∠SEP+∠SPE=∠HSP=45°,
∴∠EPS=20°,即 ∠NPK=20°.