题目内容
 如图,在平面直角坐标系中,函数y=
如图,在平面直角坐标系中,函数y=| k |
| x |
考点:反比例函数系数k的几何意义
专题:几何图形问题,数形结合
分析:由于函数y=
(x<0,常数k<0)的图象经过点A(-1,2),把(-1,2)代入解析式即可确定k=-2,依题意BC=-m,BC边上的高是2-n=2+
,根据三角形的面积公式得到关于m的方程,解方程即可求出m,然后把m的值代入y=-
,即可求得B的纵坐标,最后就求出点B的坐标.
| k |
| x |
| 2 |
| m |
| 2 |
| x |
解答:解:∵函数y=
(x<0,常数k<0)的图象经过点A(-1,2),
∴把(-1,2)代入解析式得2=
,
∴k=-2,
∵B(m,n)(m<-1),
∴BC=-m,当x=m时,n=
,
∴BC边上的高是2-n=2+
,
而S△ABC=
(-m)(2+
)=2,
∴m=-3,
∴把m=-3代入y=-
,
∴n=
,
∴点B的坐标是(-3,
).
| k |
| x |
∴把(-1,2)代入解析式得2=
| k |
| -1 |
∴k=-2,
∵B(m,n)(m<-1),
∴BC=-m,当x=m时,n=
| 2 |
| m |
∴BC边上的高是2-n=2+
| 2 |
| m |
而S△ABC=
| 1 |
| 2 |
| 2 |
| m |
∴m=-3,
∴把m=-3代入y=-
| 2 |
| x |
∴n=
| 2 |
| 3 |
∴点B的坐标是(-3,
| 2 |
| 3 |
点评:本题主要考查了用已知坐标系中点的坐标表示图象中线段的长度及三角形的面积,解题时要注意数形结合.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
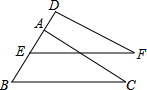 如图,△ABC≌△DEF,BE=4,AE=1,则DA的长是( )
如图,△ABC≌△DEF,BE=4,AE=1,则DA的长是( )| A、5 | B、4 | C、3 | D、2 |
 如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E,连结AE,试判断△ADE的形状,并说明理由.
如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E,连结AE,试判断△ADE的形状,并说明理由. 已知平面直角坐标系中,A(0,6),B(8,3),求满足△ABC是等腰直角三角形时点C的坐标.
已知平面直角坐标系中,A(0,6),B(8,3),求满足△ABC是等腰直角三角形时点C的坐标.