题目内容
在平面直角坐标系中有两个动点A(a,0)、B(0,a)和一个固定的点C(6,1)(a>0),若△ABC的面积是5,求a的值.
考点:三角形的面积,坐标与图形性质
专题:计算题
分析:过点C作CD⊥x轴于D,然后分a>6和a<6两种情况表示出△ABC的面积,再解关于a的方程即可得解.
解答: 解:过点C作CD⊥x轴于D,
解:过点C作CD⊥x轴于D,
①a>6时,如图1,S△ABC=
a2-
(1+a)×6-
(a-6)×1=5,
整理得,a2-7a-10=0,
解得a1=
,a2=
(舍去),
②a<6时,如图2,S△ABC=
(1+a)×6-
(6-a)×1-
a2=5,
整理得,a2-7a+10=0,
解得a1=2,a2=5,
综上所述,a的值为
或2或5.
 解:过点C作CD⊥x轴于D,
解:过点C作CD⊥x轴于D,①a>6时,如图1,S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得,a2-7a-10=0,
解得a1=
7+
| ||
| 2 |
7-
| ||
| 2 |
②a<6时,如图2,S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
整理得,a2-7a+10=0,
解得a1=2,a2=5,
综上所述,a的值为
7+
| ||
| 2 |
点评:本题考查了三角形的面积,坐标与图形性质,表示出△ABC的面积是解题的关键,难点在于分情况讨论,作出图形更形象直观.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,函数y=
如图,在平面直角坐标系中,函数y=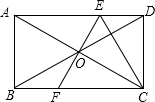 如图,矩形ABCD的周长为24cm,两条对角线相交于点O,过点O作AC的垂线EF,分别交AD,BC于点E,F,连接CE,求△CDE的周长.
如图,矩形ABCD的周长为24cm,两条对角线相交于点O,过点O作AC的垂线EF,分别交AD,BC于点E,F,连接CE,求△CDE的周长. 在一幅长90cm、宽40cm的风景画的四周外围上有一条宽度相同的金色纸边,制成一幅挂图,如果要求风景画的面积是整个挂图面积的72%,那么金边的宽应该是多少?
在一幅长90cm、宽40cm的风景画的四周外围上有一条宽度相同的金色纸边,制成一幅挂图,如果要求风景画的面积是整个挂图面积的72%,那么金边的宽应该是多少?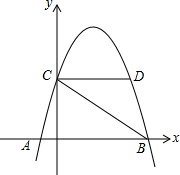 如图,抛物线y=-x2+3x+4与x轴交于A、B两点,与y轴交于点C,CD∥x轴交抛物线于点D,连接DB,在抛物线上是否存在一点P,使∠DBP=∠ABC?若存在,求出点P的坐标;若不存在,说明理由.
如图,抛物线y=-x2+3x+4与x轴交于A、B两点,与y轴交于点C,CD∥x轴交抛物线于点D,连接DB,在抛物线上是否存在一点P,使∠DBP=∠ABC?若存在,求出点P的坐标;若不存在,说明理由.