题目内容
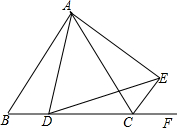 如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E,连结AE,试判断△ADE的形状,并说明理由.
如图,△ABC为等边三角形,D为BC边上一点,以AD为边作∠ADE=60°,DE与△ABC的外角平分线CE交于点E,连结AE,试判断△ADE的形状,并说明理由.考点:全等三角形的判定与性质
专题:几何图形问题
分析:过D作DG∥AC交AB于G,得出∠3=∠2,再利用AAS得出△AGD≌△DCE,进而得出答案
解答:解:△ADE是等边三角形,
理由是:过D作DG∥AC交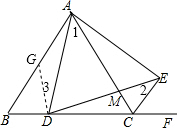 AB于G,
AB于G,
则∠1=∠3,
∵△ABC是等边三角形,
∴∠ACF=120°,
∵CE平分∠ACE,
∴∠ACE=∠ADE=60°,
∵∠AMD=∠EMC,
∴∠1=∠2=∠3,
∵∠2+∠EDC=180°-60°-60°=60°,
∴∠3+∠EDC=60°,
∵∠ADE=60°,
∴∠GDB=60°=∠B,
∴△GDB为等边三角形,
∴BG=BD,∠BGD=60°,
∵AB=BC,
∴∠AGD=∠DCE=120°,AG=DC,
在△AGD和△DCE中,
,
∴△AGD≌△DCE(AAS),
∴AD=DE,
∵∠ADE=60°,
∴△ADE是等边三角形.
理由是:过D作DG∥AC交
 AB于G,
AB于G,则∠1=∠3,
∵△ABC是等边三角形,
∴∠ACF=120°,
∵CE平分∠ACE,
∴∠ACE=∠ADE=60°,
∵∠AMD=∠EMC,
∴∠1=∠2=∠3,
∵∠2+∠EDC=180°-60°-60°=60°,
∴∠3+∠EDC=60°,
∵∠ADE=60°,
∴∠GDB=60°=∠B,
∴△GDB为等边三角形,
∴BG=BD,∠BGD=60°,
∵AB=BC,
∴∠AGD=∠DCE=120°,AG=DC,
在△AGD和△DCE中,
|
∴△AGD≌△DCE(AAS),
∴AD=DE,
∵∠ADE=60°,
∴△ADE是等边三角形.
点评:本题主要考查了全等三角形的判定与性质以及等边三角形的性质等知识,正确得出辅助线是解题关键.

练习册系列答案
相关题目
已知
,满足方程组
,则m-n的值是( )
|
|
| A、2 | B、-2 | C、0 | D、-1 |
某校为了了解学生在校午餐所需的时间,抽量了20名学生在校午餐所需时间,获得如下的数据(单位:分):10、12、15、10、16、18、19、18、20、18、18、20、28、22、30、20、15、16、21、16.若将这些数据以4分为组距进行分组,则组数是( )
| A、4组 | B、5组 | C、6组 | D、7组 |
下列各式中正确的是( )
A、
| ||||||
B、2+
| ||||||
C、
| ||||||
D、2
|
下列运算中正确的是( )
| A、2a-a=2 |
| B、m6÷m2=m3 |
| C、x2013+x2013=2x2013 |
| D、t2÷t3=t6 |
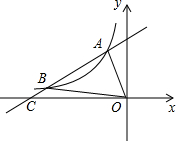 如图,一次函数y=kx+
如图,一次函数y=kx+ 如图,在平面直角坐标系中,函数y=
如图,在平面直角坐标系中,函数y=