题目内容
 已知平面直角坐标系中,A(0,6),B(8,3),求满足△ABC是等腰直角三角形时点C的坐标.
已知平面直角坐标系中,A(0,6),B(8,3),求满足△ABC是等腰直角三角形时点C的坐标.考点:等腰三角形的判定,坐标与图形性质
专题:几何综合题
分析:分当A是直角三角形的直角顶点时,当C在AB的下侧或上侧;以及当B是直角三角形的直角顶点时,当C在AB的下侧或上侧;以及当C是直角三角形的直角顶点时,当C在AB的下侧或上侧共6种情况进行讨论,利用全等三角形的判定与性质以及相似三角形的性质即可求解.
解答:解:1)当A是直角三角形的直角顶点时,当C在AB的下侧时,设是C1,作BD⊥y轴于点D,作C1E⊥y轴于点D.
∵∠C1AE+∠BAD=90°,
又∵直角△AC1E中,∠C1AE+∠C1=90°,
∴∠C1=∠BAD,
在△AC1E和△BAD中,
,
∴△AC1E≌△BAD,
∴C1E=AD,AE=BD,
∵A(0,6),B(8,3),
∴C1E=AD=6-3=3,AE=BD=8,
∴OE=AE-OA=8-6=2,
∴C1的坐标是(-3,-2);
2)当A是直角三角形的直角顶点时,当C在AB的下侧时,设是C2,此时与C1关于A对称,则C2的坐标是:(3,14);
3)当B是直角三角形的直角顶点,当C在AB的下侧时,设是C3,作C3F⊥BD于点F,同1)可得:△AC1E≌△C3FB,
则BF=C1E=3,C3F=AE=8,
则C3的坐标是:(5,-5);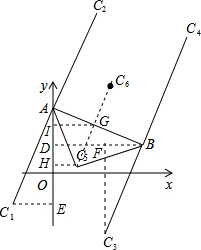
4)当B是直角三角形的直角顶点,当C在AB的上侧时,设是C4,
则B是C3C4的中点,设C4的坐标是(x,y),则
=8,
=3,
解得:x=13,y=11,
则C4的坐标是(13,11);
5)当C是直角顶点,则C一定在AB的中垂线上,在AB的下方时,设为C5,作C5H⊥y轴于H,过AB的中点G作GI⊥y轴于点I.
则△AHC5∽△GIA,且相似比是:
=
,GI=4,
∴
=
=
,
∴AH=
IG=4
,
∴OH=OA-AH=6-4
,HG=
AI=
,
∴C5的坐标是:(
,6-4
);
6)当C是直角顶点,则C一定在AB的中垂线上,在AB的上方时,设是C6,C5和C6关于G(4,
)对称,方法同4)即可求得C6的坐标是(
,3+4
).
总之,C的坐标是:(-3,-2)或(3,14)或(5,-5)或(13,11)或(
,6-4
)或(
,3+4
).
∵∠C1AE+∠BAD=90°,
又∵直角△AC1E中,∠C1AE+∠C1=90°,
∴∠C1=∠BAD,
在△AC1E和△BAD中,
|
∴△AC1E≌△BAD,
∴C1E=AD,AE=BD,
∵A(0,6),B(8,3),
∴C1E=AD=6-3=3,AE=BD=8,
∴OE=AE-OA=8-6=2,
∴C1的坐标是(-3,-2);
2)当A是直角三角形的直角顶点时,当C在AB的下侧时,设是C2,此时与C1关于A对称,则C2的坐标是:(3,14);
3)当B是直角三角形的直角顶点,当C在AB的下侧时,设是C3,作C3F⊥BD于点F,同1)可得:△AC1E≌△C3FB,
则BF=C1E=3,C3F=AE=8,
则C3的坐标是:(5,-5);

4)当B是直角三角形的直角顶点,当C在AB的上侧时,设是C4,
则B是C3C4的中点,设C4的坐标是(x,y),则
| 3+x |
| 2 |
| -5+y |
| 2 |
解得:x=13,y=11,
则C4的坐标是(13,11);
5)当C是直角顶点,则C一定在AB的中垂线上,在AB的下方时,设为C5,作C5H⊥y轴于H,过AB的中点G作GI⊥y轴于点I.
则△AHC5∽△GIA,且相似比是:
| AC5 |
| AG |
| 2 |
∴
| AH |
| IG |
| HG |
| AI |
| 2 |
∴AH=
| 2 |
| 2 |
∴OH=OA-AH=6-4
| 2 |
| 2 |
3
| ||
| 2 |
∴C5的坐标是:(
3
| ||
| 2 |
| 2 |
6)当C是直角顶点,则C一定在AB的中垂线上,在AB的上方时,设是C6,C5和C6关于G(4,
| 9 |
| 2 |
16-3
| ||
| 2 |
| 2 |
总之,C的坐标是:(-3,-2)或(3,14)或(5,-5)或(13,11)或(
3
| ||
| 2 |
| 2 |
16-3
| ||
| 2 |
| 2 |
点评:本题考查了全等三角形的判定与性质,相似三角形的判定与性质,正确进行讨论是关键.

练习册系列答案
相关题目
下列式子正确的是( )
A、
| ||||||||||
B、
| ||||||||||
C、
| ||||||||||
D、
|
下列各式中正确的是( )
A、
| ||||||
B、2+
| ||||||
C、
| ||||||
D、2
|
 如图,一次函数y=kx+
如图,一次函数y=kx+ 如图,在平面直角坐标系中,函数y=
如图,在平面直角坐标系中,函数y=
 如图,AB、CD是⊙O的直径,AB=4,点E在AB的延长线上,EF⊥AB,EF=EB=
如图,AB、CD是⊙O的直径,AB=4,点E在AB的延长线上,EF⊥AB,EF=EB= 在一幅长90cm、宽40cm的风景画的四周外围上有一条宽度相同的金色纸边,制成一幅挂图,如果要求风景画的面积是整个挂图面积的72%,那么金边的宽应该是多少?
在一幅长90cm、宽40cm的风景画的四周外围上有一条宽度相同的金色纸边,制成一幅挂图,如果要求风景画的面积是整个挂图面积的72%,那么金边的宽应该是多少?