题目内容
 如图,长方形ABCD中,AB=3,BC=5,如果将该长方形沿对角线BD折叠,那么图中阴影部分的面积是________.
如图,长方形ABCD中,AB=3,BC=5,如果将该长方形沿对角线BD折叠,那么图中阴影部分的面积是________.
5.1
分析:首先由折叠的性质与长方形的性质,易求得△BED是等腰三角形,即可得BE=DE,然后在Rt△ABE中,利用勾股定理,即可求得BE的长,继而可求得阴影部分的面积.
解答:∵将该长方形沿对角线BD折叠,
∴∠C′BD=∠DBC,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠C′BD,
∴BE=DE,
设BE=DE=x,
∴AE=5-x,
∵四边形ABCD是长方形,
∴∠A=90°,
∴AE2+AB2=BE2,
(5-x)2+32=x2
x=3.4,
∴S△EDB= ×3.4×3=5.1.
×3.4×3=5.1.
故答案为:5.1.
点评:此题考查了折叠性质,矩形的性质,等腰三角形的判定与性质,以及勾股定理等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想与方程思想的应用.
分析:首先由折叠的性质与长方形的性质,易求得△BED是等腰三角形,即可得BE=DE,然后在Rt△ABE中,利用勾股定理,即可求得BE的长,继而可求得阴影部分的面积.
解答:∵将该长方形沿对角线BD折叠,
∴∠C′BD=∠DBC,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠ADB=∠C′BD,
∴BE=DE,
设BE=DE=x,
∴AE=5-x,
∵四边形ABCD是长方形,
∴∠A=90°,
∴AE2+AB2=BE2,
(5-x)2+32=x2
x=3.4,
∴S△EDB=
 ×3.4×3=5.1.
×3.4×3=5.1.故答案为:5.1.
点评:此题考查了折叠性质,矩形的性质,等腰三角形的判定与性质,以及勾股定理等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
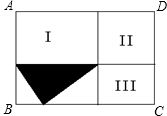 (15届江苏初二1试)已知:如图,长方形ABCD被两条线段分割成四个小长方形,如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为8、6、5,则阴影部分的面积为
(15届江苏初二1试)已知:如图,长方形ABCD被两条线段分割成四个小长方形,如果其中图形Ⅰ、Ⅱ、Ⅲ的面积依次为8、6、5,则阴影部分的面积为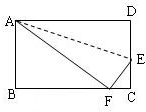 9、如图,长方形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠BAF=50°,则∠EAF的度数为( )
9、如图,长方形ABCD沿着AE折叠,使D点落在BC边上的F点处,如果∠BAF=50°,则∠EAF的度数为( )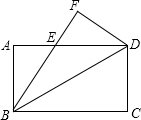 已知如图:长方形ABCD中,AB=3,BC=4,将△BCD沿BD翻折,点C落在点F处.
已知如图:长方形ABCD中,AB=3,BC=4,将△BCD沿BD翻折,点C落在点F处.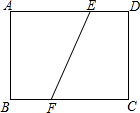 如图,长方形ABCD中,AB=3,BC=4,若将该矩形折叠,使点C与点A重合,则折痕EF的长为( )
如图,长方形ABCD中,AB=3,BC=4,若将该矩形折叠,使点C与点A重合,则折痕EF的长为( )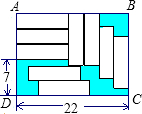 如图,长方形ABCD中放置9个形状、大小都相同的小长方形,小长方形的长为x,宽为y(尺寸如图)
如图,长方形ABCD中放置9个形状、大小都相同的小长方形,小长方形的长为x,宽为y(尺寸如图)