题目内容
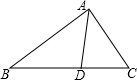 已知:如图,AD是△ABC的角平分线,且AB:AC=4:3,则△ABD与△ACD的面积之比为( )
已知:如图,AD是△ABC的角平分线,且AB:AC=4:3,则△ABD与△ACD的面积之比为( )| A、4:3 | ||
| B、16:9 | ||
C、2:
| ||
| D、9:4 |
分析:认真阅读已知条件,题目告诉了两边的比,而根据角平分线上的任意一点到角的两边距离相等,得两个三角形的高相等,于是面积比就是AB、AC的比.
解答:解:∵AD是△ABC的角平分线,
∴点D到AB和AC的距离相等,
又AB:AC=4:3,
则△ABD与△ACD的面积之比为4:3.
故选A.
∴点D到AB和AC的距离相等,
又AB:AC=4:3,
则△ABD与△ACD的面积之比为4:3.
故选A.
点评:此题主要考查角平分线的性质和三角形的面积的知识;发现并利用三角形的高相等是正确解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
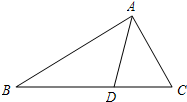 已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )| A、3:2 | B、9:4 | C、2:3 | D、4:9 |
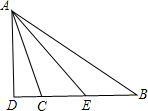 已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.
已知:如图,AD是△ABC的高,试判断∠DAE与∠B、∠ACB之间的关系,并说明理由.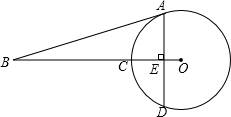
 已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF.
已知:如图,AD是一条直线,∠1=65°,∠2=115°.求证:BE∥CF. 已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.
已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.求证:GE∥AD.