Question

【题目】如图，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（﹣3，4），点C在轴的正半轴上，直线AC交轴于点M，AB边交y轴于点H，连接BM.

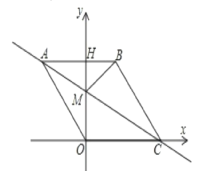
(1)菱形ABCO的边长是_________；

(2)求直线AC的解析式；

(3)动点P从点A出发，沿折线ABC的方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式.

Answer 1

【答案】（1）5；（2）y=；（3）s= t或S=t .

【解析】

（1）Rt△AOH中利用勾股定理即可求得菱形的边长；

（2）根据（1）即可求的OC的长，则C的坐标即可求得，利用待定系数法即可求得直线AC的解析式；

（3）根据S =S +S 求得M到直线BC的距离为h，然后分成P在AM上和在MC上两种情况讨论，利用三角形的面积公式求解．

(1)Rt△AOH中，

AO= =5，所以菱形边长为5；

(2)∵四边形ABCO是菱形，

∴OC=OA=AB=5,即C(5,0).

设直线AC的解析式y=kx+b，函数图象过点A. C，得

,解得 ，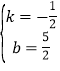

直线AC的解析式y=；

(3)设M到直线BC的距离为h，

当x=0时,y= ,即M(0, ),HM=HOOM=4=，

由S =S +S = ABOH=ABHM+BCh，

×5×4=×5×+×5h,解得h=，

①当0t<时,BP=BAAP=52t,HM=OHOM=，

s=BPHM=× (52t)= t .

②当2.5<t5时,BP=2t5,h=

S=BPh=× (2t5)= t .