ĢāÄæÄŚČŻ
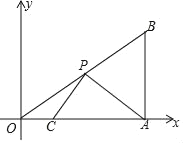
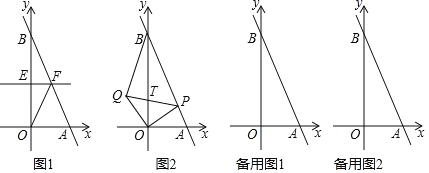
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖB£Ø0£¬b£©£Øb£¾0£©ŹĒyÖįÉĻŅ»¶Æµć£¬Ö±Ļßl¾¹żµćA£Ø1£¬0£©¼°µćB£¬½«Rt”÷ABOÕŪµž£¬Ź¹µĆµćBÓėµćOÖŲŗĻ£¬ÕŪŗŪ·Ö±š½»yÖį”¢Ö±ĻßABÓŚµćE”¢F£¬Į¬½ÓOF£®
£Ø1£©µ±b£½2Ź±£¬ĒóÖ±ĻßlµÄŗÆŹż½āĪöŹ½£»
£Ø2£©ĒėÓĆŗ¬ÓŠ×ÖÄøbµÄ“śŹżŹ½±ķŹ¾Ļ߶ĪOFµÄ³¤£¬²¢ĖµĆ÷Ļ߶ĪOFÓėĻ߶ĪABµÄŹżĮæ¹ŲĻµ£»
£Ø3£©ČēĶ¼£¬ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬ÉčµćPŹĒĻ߶ĪABÉĻŅ»¶Æµć£Ø²»ÓėA”¢BÖŲŗĻ£©£¬½«Ļ߶ĪOPČʵćOÄꏱÕėŠż×Ŗ90”ćÖĮOQ£¬Į¬½įBQ”¢PQ£¬PQ½»yÖįÓŚµćT£¬ÉčµćPµÄŗį×ų±źĪŖt£®
¢Łµ±”÷OPQµÄĆ껿×īŠ”Ź±£¬ĒóTµÄ×ų±ź£»
¢ŚČō”÷OPBŹĒµČŃüČż½ĒŠĪ£¬ĒėÖ±½ÓŠ“³öĀś×ćĢõ¼žµÄtµÄÖµ£»
¢ŪČō”÷OQBŹĒÖ±½ĒČż½ĒŠĪ£¬ĒėÖ±½ÓŠ“³öĀś×ćĢõ¼žµÄtµÄÖµ£®
”¾“š°ø”æ£Ø1£©y£½©2x+2£»£Ø2£©OF£½![]() £¬OF£½
£¬OF£½![]() AB£¬¼ū½āĪö£»£Ø3£©¢ŁT£Ø0£¬
AB£¬¼ū½āĪö£»£Ø3£©¢ŁT£Ø0£¬![]() £©£¬¢ŚtµÄÖµĪŖ
£©£¬¢ŚtµÄÖµĪŖ![]() »ņ
»ņ![]() £¬¢ŪtµÄÖµĪŖ1©
£¬¢ŪtµÄÖµĪŖ1©![]() .
.
”¾½āĪö”æ
£Ø1£©ĄūÓĆ“ż¶ØĻµŹż·Ø¼“æɽā¾öĪŹĢā£»
£Ø2£©ĄūÓĆ¹“¹É¶ØĄķĒó³öAB£¬ĄūÓĆÖ±½ĒČż½ĒŠĪŠ±±ßÖŠĻߵĊŌÖŹ¼“æɽā¾öĪŹĢā£»
£Ø3£©¢Łøł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬µ±OP”ĶABŹ±£¬”÷OPQµÄĆ껿×īŠ”£¬Ēó³öP£¬QµÄ×ų±ź£¬Ēó³öÖ±ĻßPQµÄ½āĪöŹ½¼“æɽā¾öĪŹĢā£»¢Ś·ÖĮ½ÖÖĒéŠĪ·Ö±šĒó½ā¼“æɽā¾öĪŹĢā£»¢ŪČēĶ¼5ÖŠ£¬Č”OBµÄÖŠµćG£¬Į¬½ÓBG£®ÉčP£Øt£¬-2t+2£©£¬Ēó³öµćQ×ų±ź£¬øł¾ŻQG=1¹¹½Ø·½³Ģ¼“æɽā¾öĪŹĢā£®
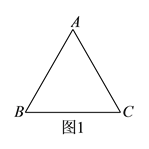
£Ø1£©ČēĶ¼1ÖŠ£¬
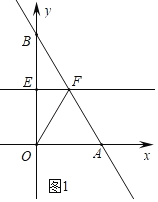
ÓÉĢāŅāA£Ø1£¬0£©£¬B£Ø0£¬2£©£¬ÉčÖ±ĻßABµÄ½āĪöŹ½ĪŖy£½kx+b£¬ŌņÓŠ![]() £¬
£¬
½āµĆ![]() £¬
£¬
”ąÖ±ĻßlµÄ½āĪöŹ½ĪŖy£½©2x+2£»
£Ø2£©ČēĶ¼1ÖŠ£¬”ßOB£½b£¬OA£½1£¬
”ąAB£½![]() £¬
£¬
”ßEF“¹Ö±Ę½·ÖĻ߶ĪBO£¬
”ąBF£½FO£¬
”ßEF”ĪOA£¬
”ąBF£½AF£¬
”ąOF£½![]() AB£½
AB£½![]() £»
£»
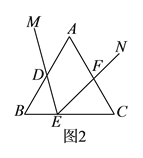
£Ø3£©¢ŁČēĶ¼2ÖŠ£¬×÷PE”ĶxÖįÓŚE£¬QF”ĶxÖįÓŚF£®
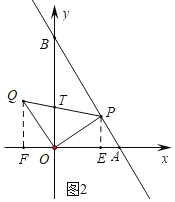
”ß”÷POQŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąµ±OPµÄÖµ×īŠ”Ź±£¬”÷POQµÄĆ껿×īŠ”£¬
øł¾Ż“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬µ±OP”ĶABŹ±£¬”÷OPQµÄĆ껿×īŠ”£¬
”ßÖ±ĻßOPµÄ½āĪöŹ½ĪŖy£½![]() x£¬
x£¬
ÓÉ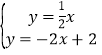 £¬
£¬
½āµĆ![]() £¬
£¬
”ąP£Ø![]() £¬
£¬![]() £©£¬
£©£¬
”ąOE£½![]() £¬PE£½
£¬PE£½![]() £¬
£¬
”ß”ĻPEO£½”ĻQFO£½”ĻPOQ£½90”ć£¬
”ą”ĻPOE+”ĻQOF£½90”ć£¬”ĻPOE+”ĻOPE£½90”ć£¬
”ą”ĻQOF£½”ĻOPE£¬
”ßOP£½OQ£¬
”ą”÷OEP”Õ”÷QFO£ØAAS£©£¬
”ąQF£½OE£½![]() £¬OF£½PE£½
£¬OF£½PE£½![]() £¬
£¬
”ąQ£Ø©![]() £¬
£¬![]() £©£¬
£©£¬
”ąÖ±ĻßPQµÄ½āĪöŹ½ĪŖy£½©![]() x+
x+![]() £¬
£¬
”ąT£Ø0£¬![]() £©£»
£©£»
¢ŚČēĶ¼3ÖŠ£¬µ±BP£½OB£½2Ź±£¬×÷PE”ĶOAÓŚE£®
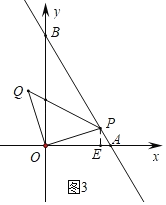
”ßPE”ĪOB£¬
”ą![]() £½
£½![]() £½
£½![]() £¬
£¬
”ą![]() £½
£½![]() £½
£½![]() £¬
£¬
”ąPE£½![]() £¬AE£½
£¬AE£½![]() £¬
£¬
”ąOE£½1©![]() £½
£½![]() £®
£®
”ąt£½![]() £®
£®
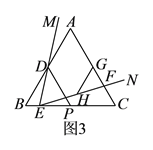
ČēĶ¼4ÖŠ£¬µ±PB£½PAŹ±£¬OP£½PBĀś×ćĢõ¼ž£¬“ĖŹ±t£½![]() £®
£®
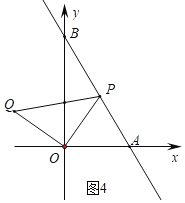
×ŪÉĻĖłŹö£¬Āś×ćĢõ¼žµÄtµÄÖµĪŖ![]() »ņ
»ņ![]() £»
£»
¢ŪČēĶ¼5ÖŠ£¬Č”OBµÄÖŠµćG£¬Į¬½ÓBG£®ÉčP£Øt£¬©2t+2£©£¬
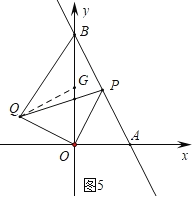
Ņ×ÖŖQ£Ø2t©2£¬t£©£¬G£Ø0£¬1£©µ±”ĻOQB£½90”揱£¬
”ßGB£½OG£¬
”ąQG£½![]() OB£½1£¬
OB£½1£¬
”ą£Ø2t©2£©2+£Øt©1£©2£½1£¬
½āµĆt£½1©![]() »ņ1+
»ņ1+![]() £ØÉįĘś£©£¬
£ØÉįĘś£©£¬
”ąĀś×ćĢõ¼žµÄtµÄÖµĪŖ1©![]() £®
£®

 Č«ÄܲāæŲĘŚÄ©Š”דŌŖĻµĮŠ“š°ø
Č«ÄܲāæŲĘŚÄ©Š”דŌŖĻµĮŠ“š°ø