题目内容
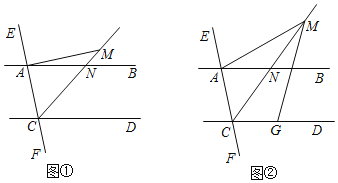
【题目】直线AB∥CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB于点N.
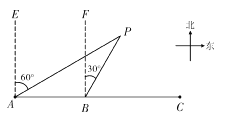
(1)如图①,过点A作AC的垂线交CM于点M,若∠MCD=55°,求∠MAN的度数;
(2)如图②,点G是CD上的一点,连接MA、MG,若MC平分∠AMG且∠AMG=36°,∠MGD+∠EAB=180°,求∠ACD的度数.

【答案】(1)∠MAN=20°;(2)∠ACD=108°.
【解析】
(1)依据角平分线的定义以及平行线的性质,即可得到∠BAC的度数,再根据垂线的定义,即可得出∠MAN的度数;
(2)设∠ACD=α,根据角平分线以及平行线即可得到∠MCG=![]() ,ACD=
,ACD=![]() α,∠BAC=∠MGD=180°-α,依据三角形外角性质,即可得到α的度数.
α,∠BAC=∠MGD=180°-α,依据三角形外角性质,即可得到α的度数.
(1)∵CM是∠ACD的平分线,∠MCD=55°,
∴∠ACD=2∠MCD=110°,
又∵AB∥CD,
∴∠BAC=180°﹣110°=70°,
又∵AM⊥EF,
∴∠MAN=90°﹣70°=20°;
(2)∵MC平分∠AMG且∠AMG=36°,
∴∠CMG=18°,
∵MC平分∠ACG,
∴∠MCG=![]() ∠ACG,
∠ACG,
∵∠CAB+∠EAB=180°,∠MGD+∠EAB=180°,
∴∠BAC=∠MGD,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
设∠ACD=α,则∠MCG=![]() ACD=
ACD=![]() α,∠BAC=∠MGD=180°﹣α,
α,∠BAC=∠MGD=180°﹣α,
∵∠MGD是△CMG的外角,
∴∠MGD=∠CMG+∠MCG,即180°﹣α=![]() α+18°,
α+18°,
解得α=108°,
∴∠ACD=108°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目