题目内容
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=90°,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕. 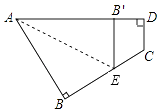
(1)试判断B′E与DC的位置关系,并说明理由;
(2)如果∠C=128°,求∠AEB的度数.
【答案】
(1)解:B′E∥DC,
证明:由折叠得:∠AB′E=∠B=∠D=90°,
∴B′E∥DC;
(2)解:∵B′E∥DC,∠C=128°,
∴∠B′EB=128°,
由折叠得:∠AEB=∠AEB′= ![]() ×128°=64°.
×128°=64°.
【解析】(1)由折叠得:∠AB′E=∠B=∠D=90°,再根据同位角相等两直线平行可得B′E∥CD;(2)根据平行线的性质求得∠B′EB,由折叠的性质得∠AEB=∠AEB′,即可求得结论.
【考点精析】本题主要考查了平行线的判定与性质和多边形内角与外角的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能正确解答此题.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?
【题目】14亿中国人与“新冠病毒”进行抗争,做为中学生的苗苗和壮壮每天都测量体温,其中10天中测量体温统计结果如下表:
姓名 | 平均数 | 中位数 | 方差 |
苗苗 | 36.1 | 36.1 | 0.50 |
壮壮 | 36.1 | 36.2 | 1.00 |
那么.这10天中体温较为稳定的是________.