题目内容
已知AB是⊙![]() 的直径,弦AC平分
的直径,弦AC平分![]() ,AD
,AD![]() CD于D,BE
CD于D,BE![]() CD于E。
CD于E。
求证:⑴CD是⊙![]() 的切线;
的切线;
⑵![]()
⑴连结OC …………………1′
∴ ∠OAC=∠OCA
∵ AC平分∠BAC
∴ ∠DAC=∠OAC
∴ ∠OCA=∠DAC …………………2′
∴ AD∥OC
∵ AD⊥CD
∴ OC⊥CD …………………3′
∴ CD是⊙的切线 …………………4′
⑵ 连结BC,延长AC交BE的延长线于M …………………5′
∵ AD⊥DE BE⊥DE
∴ AD∥BE
∴ ∠M=∠DAC
∵ ∠DAC=∠BAM
∴ ∠BAM=∠M
∴ BA=BM …………………6′
∵ AB是直径
∴ ∠ACB=90![]()
∴ AC=MC
又 ∵ ∠M=∠DAC ∠D=∠CEM AC=MC
∴ ![]()
∴ DC=EC …………………7′
(若用平行线分线段成比例定理证明,正确得分)
∴ ∠DAC=∠BCE ∠ADC=∠CEB
∴ ![]() ADC~
ADC~![]() CEB …………………8′
CEB …………………8′
∴ ![]()
![]()
∴ ![]()
∴ ![]() …………………9′
…………………9′
说明:本题还有其它证法,若正确合理得分。
解析:略

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
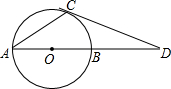 如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=
如图,已知AB是⊙O的直径,∠CAB=30°,过点C的⊙O的切线交AB延长线于D,若OD=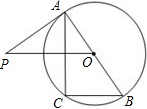 如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.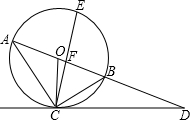

 如图,已知AB是⊙O的直径,AD切⊙O于点A,
如图,已知AB是⊙O的直径,AD切⊙O于点A,