题目内容
【题目】已知抛物线
(1)若抛物线的顶点坐标为(2，－3)，求b，c的值；
(2)若
，是否存在实数x，使得相应的y的值为1，请说明理由；
(3)若
且抛物线在－2≤x≤2上的最小值是－3，求b的值．
【答案】（1）b＝2,c＝1；
（2）存在两个不同实数
，使得相应
，理由见解析；（3）
或
【解析】分析(1) 由顶点坐标为(2，－3)化为 顶点
即可求解.(2)把y=1，c=-b,代入
化为
,根据求根公式即可求解.(3)把c=b+2代入化为
,由对称轴为
，分两种情况讨论即可.
(本小题满分12分)
解：(1
)，b＝2,c＝1 (2)由 ,b+c=0 得 
，,
所以方程 
有两个不相等实数根，
即存在两个不同实数，使得相应
(3)由c=b+2，则抛物线可化为
，其对称轴为x=b，
①当x=b<-2时，则有抛物线在
时取最小值为-3，此时
，解得
，不合题意
②当x=b>2时，则有抛物线在
时取最小值为-3，此时
，解得，合题意
当
，则
，化简得：
，解得：
(不合题意，舍去)，
.
综上：或
练习册系列答案
相关题目
【题目】在我市实施“城乡环境综合治理”期间，某校组织学生开展“走出校门，服务社会”的公益活动．八年级一班王浩根据本班同学参加这次活动的情况，制作了如下的统计图表：
该班学生参加各项服务的频数、频率统计表：
服务类别 | 频数 | 频率 |
文明宣传员 | 4 | 0.08 |
文明劝导员 | 10 | |
义务小警卫 | 8 | 0.16 |
环境小卫士 | 0.32 | |
小小活雷锋 | 12 | 0.24 |
请根据上面的统计图表，解答下列问题：
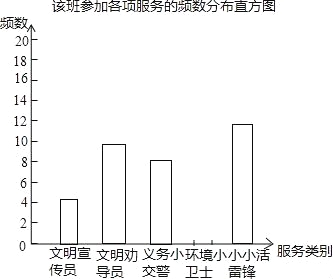
（1）该班参加这次公益活动的学生共有 名；
（2）请补全频数、频率统计表和频数分布直方图；
（3）若八年级共有900名学生报名参加了这次公益活动，试估计参加文明劝导的学生人数．
