题目内容
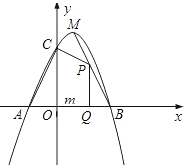
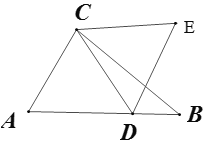
【题目】如图,在![]() 中,
中,![]() 为边
为边![]() 的中点,
的中点,![]() 为线段
为线段![]() 上一点,联结
上一点,联结![]() 并延长交边
并延长交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平分线,交射线
的平分线,交射线![]() 于点
于点![]() .设
.设![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)设![]() ,求关于
,求关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或2.
或2.
【解析】
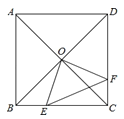
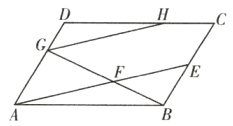
(1)由平行四边形ABCD,得到AD与BC平行且相等,由两直线平行得到两对内错角相等,进而确定出三角形BEF与三角形AGF相似,由相似得比例,把x=1代入已知等式,结合比例式得到AG=BE,AD=AB,即可求出所求式子的值;
(2)设AB=1,根据已知等式表示出AD与BE,由AD与BC平行,得到比例式,表示出AG与DG,利用两角相等的三角形相似得到三角形GDH与三角形ABE相似,利用相似三角形面积之比等于相似比的平方列出y与x的函数解析式,并求出x的范围即可;
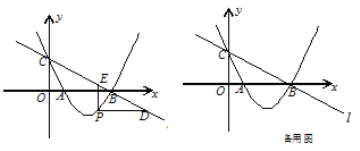
(3)分两种情况考虑:①当点H在边DC上时,如图1所示;②当H在DC的延长线上时,如图2所示,分别利用相似得比例列出关于x的方程,求出方程的解即可得到x的值.
(1)在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
![]() ,即
,即![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() 为
为![]() 的中点,
的中点,
![]() .
.
![]() ,即
,即![]() .
.
(2)![]() ,
,
![]() 不妨设
不妨设![]() .
.
则![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
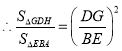 .
.
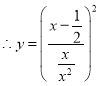 .
.
![]() .
.
(3)①当点![]() 在边
在边![]() 上时,
上时,
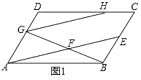
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
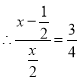 .
.
解得![]() .
.
②当![]() 在
在![]() 的延长线上时,
的延长线上时,
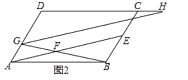
![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() .
.
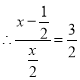 .
.
解得![]() .
.
综上所述,可知![]() 的值为
的值为![]() 或2.
或2.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目