Question

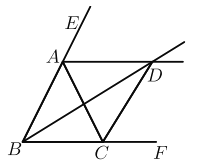
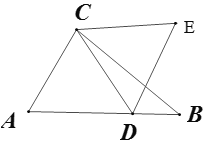
【题目】如图，△ABC中，AB=8，AC=5，BC=7，点D在AB上一动点，线段CD绕点C逆时针旋转60°得到线段CE，AE的最小值为________

Answer 1

【答案】

【解析】

以AC为边作等边△ACF，连接DF，AE，易证△ACE≌△FCD，可得AE=FD，当FD最小时，AE最小，F为定点，D为AB上动点，则FD⊥AB时，FD取得最小值，过C作CM⊥AB于M，过F作FH⊥AB于点H，设AM=x，利用勾股定理解出x=2.5，所以∠CAB=60°，可推出∠FAH=60°，求出FH即为AE的最小值.

解：如图，以AC为边作等边△ACF，连接DF，AE，

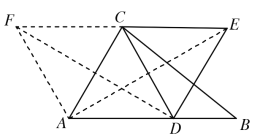
∵线段CD绕点C逆时针旋转60°得到线段CE

∴CE=CD，∠DCE=60°，

∴∠DCE+∠ACD=∠FCA+∠ACD

即∠ACE=∠FCD

在△ACE和△FCD中，

∵AC=FC，∠ACE=∠FCD，CE=CD

∴△ACE≌△FCD（SAS）

∴AE=FD

当FD⊥AB时，FD取得最小值，即为AE的最小值，

如图，过C作CM⊥AB于M，过F作FH⊥AB于点H，

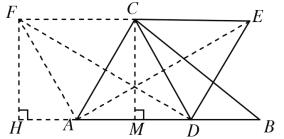
设AM=x，∵AB=8，AC=5，BC=7

∴BM=8-x，

在Rt△ACM和Rt△BCM中，

∴

解得

∴

∴∠ACM=30°，∠CAM=60°，

∴∠FAH=180°-60°-60°=60°

∴∠AFH=30°，

∴，

∴AE的最小值=FH=.

故答案为：.