题目内容
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,BD=CE. 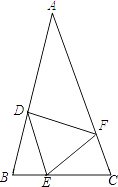
(1)求证:△DEF是等腰三角形;
(2)求证:∠B=∠DEF;
(3)当∠A=40°时,求∠DEF的度数.
【答案】
(1)证明:∵AB=AC,
∴∠B=∠C,
在△DBE和△ECF中, 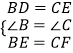 ,
,
∴△DBE≌△ECF,
∴DE=FE,
∴△DEF是等腰三角形
(2)证明:∵△BDE≌△CEF,
∴∠FEC=∠BDE,
∴∠DEF=180°﹣∠BED﹣∠EFC=180°﹣∠DEB﹣∠EDB=∠B
(3)证明:∵由(2)知△BDE≌△CEF,
∴∠BDE=∠CEF,
∴∠CEF+∠DEF=∠BDE+∠B,
∴∠DEF=∠B,
∴AB=AC,∠A=40°,
∴∠DEF=∠B= ![]() =70°
=70°
【解析】(1)首先根据条件证明△DBE≌△ECF,根据全等三角形的性质可得DE=FE,进而可得到△DEF是等腰三角形;(2)根据△BDE≌△CEF,可知∠FEC=∠BDE,∠DEF=180°﹣∠BED﹣∠EFC=180°﹣∠DEB﹣∠EDB=∠B即可得出结论;(3)由(2)知∠DEF=∠B,再根据等腰三角形的性质即可得出∠DEF的度数.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】下表是初二年级50名同龄女生身高数据:
身高/cm | 146 | 151 | 153 | 154 | 156 | 157 | 158 | 159 | 160 |
人数 | 1 | 2 | 2 | 2 | 3 | 4 | 8 | 4 | 4 |
身高/cm | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 169 | |
人数 | 2 | 4 | 3 | 2 | 3 | 4 | 1 | 1 |
(1)根据下表的分组方法进行数据整理,补全频数分布表:
(2)根据分布表画出频数分布直方图.
(3)观察频数分布表和频数分布直方图回答问题:为了参加广播操比赛,老师打算从以上50名女生中挑选30名队员。为了让参赛队员的身高比较整齐,老师应该选择身高在什么范围内的同学呢?请写出答案并简述理由.