题目内容

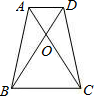
如图，在梯形ABCD中，AB∥CD，AD=BC，对角线AC⊥BD，垂足为O．若CD=3，AB=5，则AC的长为______，CB长为______．
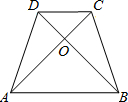
过点C作CE∥DB交AB的延长线于点E，过点C作CF⊥AB交AB于点F，

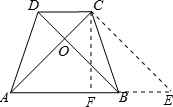
∵AD=BC，AC⊥BD，AB∥CD，
∴四边形DCEB是平行四边形，四边形ABCD是等腰梯形，△ACE是等腰直角三角形，
∴BF=
1
2
（AB-DC）=1，
在RT△ACE中，可得AC=AEsin45°=4
2
；
在RT△BFC中，BC=
CF2+BF2
=
17
．
故答案为：4
2
，
17
．
练习册系列答案
相关题目
如图，E点为△ABC的边AC中点，CN∥AB，过E点作直线交AB与M点，交CN于N点，若MB=6cm，CN=4cm，则AB=______cm．
在等腰梯形ABCD中，AD∥BC，AD=1，AB=CD=2，BC=3，则∠B=______度．
如图，梯形ABCD中，AB∥CD，△ABD为等腰直角三角形，∠ADB=90゜，AC=AB，AC与BD相交于E点，CF⊥AB于点F，交BD于G点．下列结论：
①CF=
1
2
AB；②BE=BC；③BC=
2
CD；④CE=2BF，
其中正确的个数为（　　）
A．1个B．2个C．3个D．4个
如图，在等腰梯形ABCD中，AD∥BC，AD=3，BC=5，AC、BD相交于O点，且∠BOC=60°，顺次连接等腰梯形各边中点所得四边形的周长是（　　）
A．24B．20C．16D．12
如图1，直线L为?ABCD外一条直线，分别过A、B、C、D作L垂线段，AA1、BB1、CC1、DD1，那么，将有AA1+CC1=BB1+DD1，现在若将L向上平移，使L与?ABCD相交（如图2），若其他条件不变，猜想线段AA2、BB2、CC2、DD2的数量关系是______
如图所示，在梯形ABCD中，已知AD∥BC，AB=DC，∠ACB=40°，∠ACD=30°．
（1）∠BAC=______°；
（2）如果BC=5cm，连接BD，求AC、BD的长度．
从边长为a的大正方形纸板中间挖去一个边长为b的小正方形后，将其截成四个相同的等腰梯形﹙如图①﹚，可以拼成一个平行四边形﹙如图②﹚．
现有一平行四边形纸片ABCD﹙如图③﹚，已知∠A=45°，AB=6，AD=4．若将该纸片按图②方式截成四个相同的等腰梯形，然后按图①方式拼图，则得到的大正方形的面积为______．
在等腰梯形ABCD中，AB=CD，DC=BC，E是BA、CD延长线的交点，∠E=40°，则∠ACD=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网