题目内容
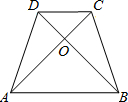
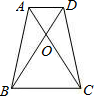
如图，在等腰梯形ABCD中，AD∥BC，AD=3，BC=5，AC、BD相交于O点，且∠BOC=60°，顺次连接等腰梯形各边中点所得四边形的周长是（ ）
| A．24 | B．20 | C．16 | D．12 |
∵梯形ABCD是等腰梯形，
∴AC=BD，AB=CD，BC=BC，
∴△ABC≌△DCB，
∴∠BAC=∠BDC，
∵∠AOB=∠COD，
∴∠ABD=∠ACD，
∵AB=CD，
∴△AOB≌△DOC，
∴OB=OC，
∵在△BOC中，∠BOC=60°，∠OBC=∠OCB=
（180°-60°）=60°，
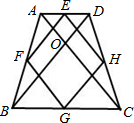
∴OB=OC=BC=5，同理AO=DO=AD=3，则AC=BD=3+5=8，根据中位线定理，FG=GH=HE=EF=8×
=4，四边形的周长是4×4=16，
故选C．
∴AC=BD，AB=CD，BC=BC，
∴△ABC≌△DCB，
∴∠BAC=∠BDC，
∵∠AOB=∠COD，
∴∠ABD=∠ACD，
∵AB=CD，
∴△AOB≌△DOC，
∴OB=OC，
∵在△BOC中，∠BOC=60°，∠OBC=∠OCB=
| 1 |
| 2 |
∴OB=OC=BC=5，同理AO=DO=AD=3，则AC=BD=3+5=8，根据中位线定理，FG=GH=HE=EF=8×
| 1 |
| 2 |
故选C．
练习册系列答案
轻松暑假总复习系列答案
相关题目
到达顶点时，另一点也随之停止运动，设运动时间为t（s），问t为何值时，
