题目内容
13、在Rt△ABC和Rt△A′B′C′中(其中∠C=∠C′=90°),下列条件:
①AC=A′C′,∠A=∠A′;②AC=A′C′,BC=B′C′;③∠A=∠A′,∠B=∠B′;④∠B=∠B′.AB=A′B′;⑤AC=A′C′,AB=A′B′中,能判定两个三角形全等的是
①AC=A′C′,∠A=∠A′;②AC=A′C′,BC=B′C′;③∠A=∠A′,∠B=∠B′;④∠B=∠B′.AB=A′B′;⑤AC=A′C′,AB=A′B′中,能判定两个三角形全等的是
①②④⑤
.分析:此题是一道开放性题,实则还是考查学生对三角形全等的判定方法的掌握情况.此处可以运用排除法进行分析.
解答:解:①AC=A′C′,∠A=∠A′,符合ASA,能判定;
②AC=A′C′,BC=B′C′,符合SAS,能判定;
③∠A=∠A′,∠B=∠B′,是AAA,不能判定;
④∠B=∠B′,AB=A′B′,符合AAS,能判定;
⑤AC=A′C′,AB=A′B′,符合HL,能判定.
故填①②④⑤.
②AC=A′C′,BC=B′C′,符合SAS,能判定;
③∠A=∠A′,∠B=∠B′,是AAA,不能判定;
④∠B=∠B′,AB=A′B′,符合AAS,能判定;
⑤AC=A′C′,AB=A′B′,符合HL,能判定.
故填①②④⑤.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
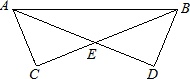 23、已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.
23、已知:如图,在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC,AD相交于点E.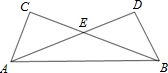 已知:如图在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC与AD相交于点E.
已知:如图在Rt△ABC和Rt△BAD中,AB为斜边,AC=BD,BC与AD相交于点E.
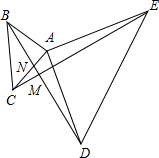 如图,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,CE与BD相交于点M,BD交AC于点N.试猜想BD与CE有何关系?并证明你的猜想.
如图,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,CE与BD相交于点M,BD交AC于点N.试猜想BD与CE有何关系?并证明你的猜想.