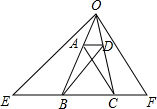
题目内容
在梯形ABCD中,两底AB=14cm,CD=6cm,两底角∠A=30°,∠B=60°,则腰BC的长为
- A.8cm
- B.6cm
- C.4cm
- D.3cm
C
分析:延长两腰交于点E,则得到直角三角形ABE和直角三角形CDE,利用三角函数即可求得BE,CE的长,则BC的长就不难得到了.
解答: 解:延长两腰交于点E
解:延长两腰交于点E
在直角三角形ABE中,
∵∠A=30°,AB=14
∴BE=7
在直角三角形CDE中
∵∠CDE=30°,CD=6
∴CE=3
∴BC=BE-CE=7-3=4
故选C.
点评:注意梯形中常见的辅助线之一:延长两腰.此题中构造了两个30°的等腰直角三角形,根据30°所对的直角边是斜边的一半进行计算.
分析:延长两腰交于点E,则得到直角三角形ABE和直角三角形CDE,利用三角函数即可求得BE,CE的长,则BC的长就不难得到了.
解答:
 解:延长两腰交于点E
解:延长两腰交于点E在直角三角形ABE中,
∵∠A=30°,AB=14
∴BE=7
在直角三角形CDE中
∵∠CDE=30°,CD=6
∴CE=3
∴BC=BE-CE=7-3=4
故选C.
点评:注意梯形中常见的辅助线之一:延长两腰.此题中构造了两个30°的等腰直角三角形,根据30°所对的直角边是斜边的一半进行计算.

练习册系列答案
相关题目
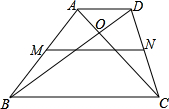 如图在梯形ABCD中,两对角线AC、BD互相垂直于O点,且AC=6、BD=8,试求梯形ABCD的中位线MN及高h的长.
如图在梯形ABCD中,两对角线AC、BD互相垂直于O点,且AC=6、BD=8,试求梯形ABCD的中位线MN及高h的长.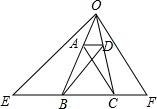 如图所示.在梯形ABCD中,两腰BA,CD的延长线相交于O,OE∥DB,OF∥AC且分别交直线BC于E,F.求证:BE=CF.
如图所示.在梯形ABCD中,两腰BA,CD的延长线相交于O,OE∥DB,OF∥AC且分别交直线BC于E,F.求证:BE=CF.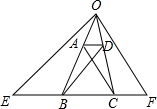 如图所示.在梯形ABCD中,两腰BA,CD的延长线相交于O,OE∥DB,OF∥AC且分别交直线BC于E,F.求证:BE=CF.
如图所示.在梯形ABCD中,两腰BA,CD的延长线相交于O,OE∥DB,OF∥AC且分别交直线BC于E,F.求证:BE=CF.